题目内容
17. 如图所示,在高h=1.8m的光滑水平桌面上,固定一半径为r=0.4m的$\frac{3}{4}$光滑圆弧槽轨道,轨道一端与桌边缘相切于B点,一小球从A点以v0=2m/s的速度沿圆弧槽运动,从C点离开圆轨道,求:(tan30°=$\frac{\sqrt{3}}{3}$,tan60°=$\sqrt{3}$,取g=10m/s2)
如图所示,在高h=1.8m的光滑水平桌面上,固定一半径为r=0.4m的$\frac{3}{4}$光滑圆弧槽轨道,轨道一端与桌边缘相切于B点,一小球从A点以v0=2m/s的速度沿圆弧槽运动,从C点离开圆轨道,求:(tan30°=$\frac{\sqrt{3}}{3}$,tan60°=$\sqrt{3}$,取g=10m/s2)(1)小球在圆弧槽轨道AC间运动的角速度是多少;
(2)小球从C点离开圆弧槽轨道到落地时所需的时间;
(3)小球落地时速度方向和水平面夹角是否大于60°?(通过计算得出)
分析 根据圆周运动的角速度公式分析求解;
根据平抛运动的规律求解时间;
根据平抛运动的规律求出小球落地时速度方向和水平面夹角的正切值进行判断求解;
解答 解:(1)小球从A点以v0=2m/s的速度沿圆弧槽运动,半径为r=0.4m的$\frac{3}{4}$光滑圆弧槽轨道,
根据圆周运动的角速度公式得
ω=$\frac{{v}_{0}}{r}$=5rad/s,
(2)小球从C点离开圆弧槽轨道到落地,先做匀速直线运动,再做平抛运动,
r=v0t
根据平抛运动的规律得h=$\frac{1}{2}$gt′2
小球从C点离开圆弧槽轨道到落地时所需的时间t总=t+t′=0.8s,
(3)根据平抛运动的规律得:
小球落地时速度方向和水平面夹角的正切值tanθ=$\frac{gt′}{{v}_{0}}$=3>tan60°=$\sqrt{3}$
所以小球落地时速度方向和水平面夹角大于60°.
答:(1)小球在圆弧槽轨道AC间运动的角速度是5rad/s,
(2)小球从C点离开圆弧槽轨道到落地时所需的时间是0.8s;
(3)小球落地时速度方向和水平面夹角大于60°.
点评 本题是匀速圆周运动、匀速直线运动和平抛运动的组合,记住匀速圆周运动的角速度、加速度等等公式,就可以轻松解答.

练习册系列答案
相关题目
8.如图,在同一竖直平面内,距地面不同高度的地方,以不同的水平速度同时抛出两个小球,则( )

| A. | 两球一定不能在空中相遇 | |
| B. | 两球落地时间可能相等 | |
| C. | 两球抛出到落地的水平距离有可能相等 | |
| D. | 两球运动的水平距离与抛出点的高度无关 |
5. 如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )
如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )
 如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )
如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )| A. | 做匀速运动 | B. | 做匀变速曲线运动 | ||
| C. | 受到的合外力为零 | D. | 加速度大小保持不变 |
12. “神舟九号”与“天宫一号”在对接前,在各自轨道上运行,它们的轨道如图所示,假定它们都做匀速圆周运动,则( )
“神舟九号”与“天宫一号”在对接前,在各自轨道上运行,它们的轨道如图所示,假定它们都做匀速圆周运动,则( )
 “神舟九号”与“天宫一号”在对接前,在各自轨道上运行,它们的轨道如图所示,假定它们都做匀速圆周运动,则( )
“神舟九号”与“天宫一号”在对接前,在各自轨道上运行,它们的轨道如图所示,假定它们都做匀速圆周运动,则( )| A. | 宇航员在“神舟九号”上不受地球引力作用 | |
| B. | “天宫一号”的运行周期比“神舟九号”长 | |
| C. | “天宫一号”的加速度比“神舟九号”大 | |
| D. | “神舟九号”运行速度较大,要减速才能与“天宫一号”对接 |
2. 电磁轨道炮工作原理如图所示.待发射弹体可在两平行轨道之间自由移动,并与轨道保持良好接触.电流I从一条轨道流入,通过导电弹体后从另一条轨道流回.轨道电流在弹体处形成垂直于轨道面的磁场(可视为匀强磁场),磁感应强度的大小与I成正比.通电的弹体在轨道上受到安培力的作用而高速射出.现欲使弹体的出射速度增加至原来的2倍,理论上可采用的办法是( )
电磁轨道炮工作原理如图所示.待发射弹体可在两平行轨道之间自由移动,并与轨道保持良好接触.电流I从一条轨道流入,通过导电弹体后从另一条轨道流回.轨道电流在弹体处形成垂直于轨道面的磁场(可视为匀强磁场),磁感应强度的大小与I成正比.通电的弹体在轨道上受到安培力的作用而高速射出.现欲使弹体的出射速度增加至原来的2倍,理论上可采用的办法是( )
 电磁轨道炮工作原理如图所示.待发射弹体可在两平行轨道之间自由移动,并与轨道保持良好接触.电流I从一条轨道流入,通过导电弹体后从另一条轨道流回.轨道电流在弹体处形成垂直于轨道面的磁场(可视为匀强磁场),磁感应强度的大小与I成正比.通电的弹体在轨道上受到安培力的作用而高速射出.现欲使弹体的出射速度增加至原来的2倍,理论上可采用的办法是( )
电磁轨道炮工作原理如图所示.待发射弹体可在两平行轨道之间自由移动,并与轨道保持良好接触.电流I从一条轨道流入,通过导电弹体后从另一条轨道流回.轨道电流在弹体处形成垂直于轨道面的磁场(可视为匀强磁场),磁感应强度的大小与I成正比.通电的弹体在轨道上受到安培力的作用而高速射出.现欲使弹体的出射速度增加至原来的2倍,理论上可采用的办法是( )| A. | 只将弹体质量减至原来的一半 | |
| B. | 只将电流I增加至原来的2倍 | |
| C. | 只将轨道长度L变为原来的2倍 | |
| D. | 将弹体质量减至原来的一半,轨道长度L变为原来的4倍,其它量不变 |
6.将一只小球竖直上抛,当它到达最高点时速度为零,加速度的方向是( )
| A. | 方向从向上变为向下 | B. | 方向从向下变向上 | ||
| C. | 方向向上 | D. | 方向向下 |
7.电场中某区域的电场线分布如图所示,下列说法正确是( )


| A. | A点的电势高 | B. | B点的电势高 | C. | A点的电场强度小 | D. | B点的电场强度小 |
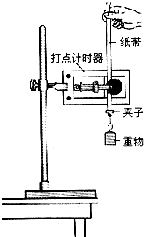 某同学在做“验证机械能守恒定律”的实验中,列出下面一些步骤:
某同学在做“验证机械能守恒定律”的实验中,列出下面一些步骤: