题目内容
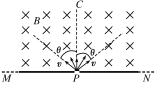
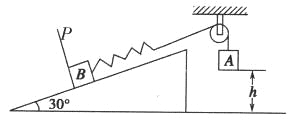
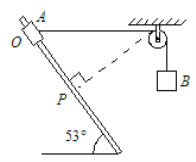
【题目】有一个固定的光滑直杆与水平面的夹角为 53°,杆上套着一个质量为m= 2kg 的滑块 A(可视为质点).用不可伸长的轻绳将滑块A与另一个质量为M=2.7kg 的物块B通过光滑的定滑轮相连接,细绳因悬挂B而绷紧,此时滑轮左侧轻绳恰好水平,其长度![]() m,P点与滑轮的连线同直杆垂直(如图所 示).现将滑块A从图中O点由静止释放,(整个运动过程中 B不会触地,g=10m/s2)。下列说法正确的是
m,P点与滑轮的连线同直杆垂直(如图所 示).现将滑块A从图中O点由静止释放,(整个运动过程中 B不会触地,g=10m/s2)。下列说法正确的是
A. 滑块A运动到 P点时加速度为零
B. 滑块A由O点运动到P点的过程中机械能增加
C. 滑块A经过 P点的速度大小为5![]() m/s
m/s
D. 滑块A经过P点的速度大小为![]() m/s
m/s
【答案】BC
【解析】
A、滑块A运动到P点时,垂直于杆子的方向受力平衡,合力为零;沿杆子方向,重力有沿杆向下的分力mgsin53°,根据牛顿第二定律得:mgsin53°=ma,a=gsin53°,故A错误。
B、滑块A由O点运动到P点的过程中,绳子的拉力对滑块A做正功,其机械能增加;故B正确。
C、D、由于图中杆子与水平方向成53°,可以解出图中虚线长度:![]() ,所以滑块A运动到P时,A下落
,所以滑块A运动到P时,A下落![]() ,B下落
,B下落![]() ,当A到达P点与A相连的绳子此时垂直杆子方向的速度为零,则B的速度为零,以两个物体组成的系统为研究对象,由机械能守恒定律得:
,当A到达P点与A相连的绳子此时垂直杆子方向的速度为零,则B的速度为零,以两个物体组成的系统为研究对象,由机械能守恒定律得:![]() ,解得
,解得![]() ;故C正确,D错误。
;故C正确,D错误。
故选BC。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目