��Ŀ����
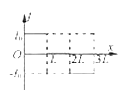
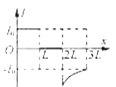
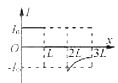
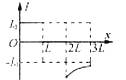
����Ŀ������֥�����Ǵ������Ͽ����ģ����Ǿ�������֥�鿪���ڽڸ����������Dz�������������Խ��Խ��֮�⡣ͨ�����Ƶ糡�ʹų����������ô������ӵ��˶��켣�����֥�鿪���ڽڸ����ľ�����ͼ�ף��ڵ���MN�·�����ֱ���µ���ǿ�糡��һ������Ϊm��10��3kg�������q����0.1C������v��2m/s���������˶���ѡȡ���˶������뵲��L��5m��O��Ϊ��ʱ�̣�ʩ��һ����ͼ���������Ա仯�Ĵų����Ÿ�Ӧǿ�ȴ�СΪB��0.1T��ѡ��ֱֽ������Ϊ�ų����������������ٶ�g��10m/s2������������������ʾ������
��1���糡ǿ�ȵĴ�С��
��2����������t��2sʱ����O����룻
��3����������O�㵽������Ҫ��ʱ�䡣
���𰸡���1��0.1N/C��2����4��0.8����m��3����2.5+1.2����s
��������
��1�������������˶���������ƽ���֪��qE��mg
�������ݽ�ã�E��0.1N/C
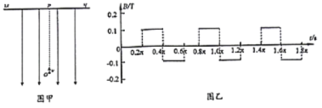
��2�����˴ų��������������糡������������������������Բ���˶��������������ṩ����������![]()
�������ݽ�ã�R��0.2m
���˶�һ�ܵ�ʱ��T����![]()
��ã�T����0.2����s
���ͼ�ҿɻ������˶��켣������0.6����2��0.8���������������������˶�������O�����h
����h��v��t��2T��
��ã�h����4��0.8����m
��3������O�㵽�������1.2����5��1.6������������O�㵽������Ҫ��ʱ��t0
��t0��![]() +6T
+6T
�������ݽ��t0����2.5+1.2����s

 ��У����ϵ�д�
��У����ϵ�д�