Question

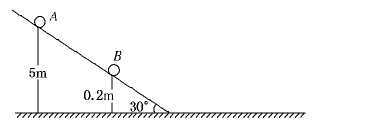
小物块A的质量为m,物块与坡道间的动摩擦因数为μ,水平面光滑；坡道顶端距水平面高度为h，倾角为θ;物块从坡道进入水平滑道时，在底端O点处无机械能损失，重力加速度为g.将轻弹簧的一端连接在水平滑道M处并固定在墙上，另一自由端恰位于坡道的底端O点，如图所示.物块A从坡顶由静止滑下，

求：（1）物块滑到O点时的速度大小；
（2）弹簧为最大压缩量d时的弹性势能；
（3）物块A被弹回到坡道上升的最大高度.

Answer 1

(1)由动能定理得
mgh-μmghcotθ=，①
得.    （4分）
(2)在水平滑道上
由能量守恒定律得=E_p，②
解得E_p=mgh-μmghcotθ.（4分）
（3）设物块A能够上升的最大高度为h₁,物块A被弹回过程中
由能量守恒定律得E_p=μmgh₁cotθ+mgh₁，③
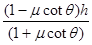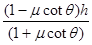解得h₁=.（4分）

试题分析：题目时要注意一些比较关键的信息词：光滑，无机械能损失。这些都意味着没有摩擦力做功。所以本题可以考虑使用机械能守恒定律。但是在有摩擦力的地方，应该优先使用动能定理。
考点分析：动能定理、能量守恒定律
总结评价：本题的最终问题对大多数同学来说可能较难回答，通过中间的（1）（2）两问，明显缩小了思维难度，能够让大多数同学回答得出。因此平日我们做题思考应该像这个题目一样，多设问一些问题，降低思维难度。