题目内容
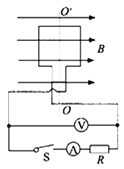
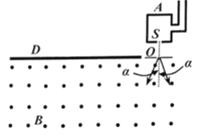
【题目】如图为近代物理实验室中研究带电粒子的一种装置。带正电的粒子从容器A下方的小孔S不断飘入电压为U的加速电场，经过S正下方的小孔O后，沿SO方向垂直进入磁感应强度为B、方向垂直纸面向外的匀强磁场中，最后打在相机底片D上并被吸收。已知D与O在同一平面内，粒子在D上的落点到O的距离为x，不考虑粒子重力和粒子在小孔S处的速度。
(1)求粒子的比荷
；
(2)由于粒子间存在相互作用，从O进入磁场的粒子在纸面内将发生不同程度的微小偏转，其方向与竖直方向的最大偏角为α，若粒子速度大小相同，求粒子在D上的落点到O的距离最大值和最小值；
(3)实际上，加速电场的电压也会发生微小变化（设电压变化范围为U±ΔU），从而导致进入磁场的粒子的速度大小也有所不同。现从容器A中飘入的粒子电荷量相同但质量分别为m1、m2 (m1>m2)，最终均能打在D上，若要使这两种粒子的落点区域不重叠，则ΔU应满足什么条件？（粒子进入磁场时的速度方向与竖直方向的最大偏角仍为α）
【答案】（1）
（2）最大值
最小值
（3）
【解析】（1）沿SO方向垂直进入磁场的粒子，最后打在照相底片D的粒子；
粒子经过加速电场：qU=
mv2
洛伦兹力提供向心力：qvB=m
落点到O的距离等于圆运动直径：x=2R
所以粒子的比荷为：
（2）粒子在磁场中圆运动半径
由图象可知：粒子左偏θ角（轨迹圆心为O1）或右偏θ角（轨迹圆心为O2）
落点到O的距离相等，均为L=2Rcosθ
故落点到O的距离
最大：Lmax=2R=x
最小：Lmin=2Rcosα=xcosα
（3）①考虑同种粒子的落点到O的距离；
当加速电压为U+△U、偏角θ=0时，距离最大，
Lmax=2Rmax=
当加速电压为U-△U、偏角θ=α时，距离最小
Lmin=2Rmincosα=
cosα
②考虑质量不同但电荷量相同的两种粒子
由R=
和m1＞m2，知：R1＞R2
要使落点区域不重叠，则应满足：L1min＞L2max
cosα＞
