题目内容
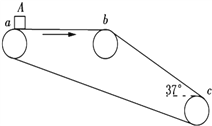
【题目】如图，质量均为2m的木板A、B并排静止在光滑水平地面上，A左端紧贴固定于水平面的半径为R的四分之一圆弧底端，A与B、A与圆弧底端均不粘连。质量为m的小滑块C从圆弧顶端由静止滑下，经过圆弧底端后，沿A的上表面从左端水平滑上A，并在恰好滑到B的右端时与B一起匀速运动。已知重力加速度为g，C过圆弧底端时对轨道的压力大小为1.5mg，C在A、B上滑行时受到的摩擦阻力相同，C与B一起匀速的速度是C刚滑上A时的0.3倍。求：
(1)C从圆弧顶端滑到底到的过程中克服摩擦力做的功；
(2)两板长度L1与L2之比。
(3)C刚滑到B的右端时，A右端到B左端的水平距离s与`的长度L2之比。
【答案】(1) 
(2) 
(3) 
【解析】（1）设C到达圆弧底端时的速度为v0，轨道对C支持力大小为N，下滑过程C克服摩擦力做的功为Wf。由动能定理，有：
①
C过底端时，由牛顿第二定律，有：
②
由牛顿第三定律，知： 
③
联立①②③式得： 
④
（2）设C刚滑过A到达B时，C的速度为vC，A、B的速度为v，B、C共同速度为vBC，C与A、B间的摩擦力为f。
C从滑上A到刚滑到B这个过程，C和A、B组成的系统动量守恒。
由动量守恒守律： 
⑤
由功能关系： 
⑥
C滑上B到与B共速这个过程，对C和B组成的系统，
由动量守恒定律： 
⑦
由功能关系： 
⑧
或：C从滑上A到与B共速的全过程
由动量守恒定律： 
⑨
由功能关系： 
⑩
⑤⑦⑨任两式联立并代入
得： 
⑥⑧⑩任两式联立并代入
得： 
（3）设C从滑上B到与B共速所经历的时间为t，
对B，由动量定理： 
在t时间内，A通过的距离： 
设B在t时间内通过的距离为sB，
对B应用动能定理： 
联立⑧⑩
式并代入
， 
得：
练习册系列答案
相关题目
