题目内容
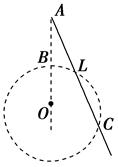
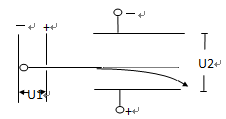
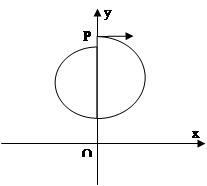
(22分)如图所示,在xoy平面内第二象限的某区域存在一个圆形匀强磁场区,磁场方向垂直xoy平面向外。一电荷量为e、质量为m的电子,从坐标原点O处以速度v0射入第二象限,速度方向与y轴正方向成30°角,经过磁场偏转后,通过P(0,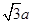 )点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为
)点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为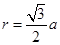 ,求:
,求:

(1)电子从坐标原点O 运动到P点的时间t1;
(2)所加圆形匀强磁场区域的最小面积;
(3)若电子到达y轴上P点时,撤去圆形匀强磁场,同时在y轴右侧加方向垂直xoy平面向里的匀强磁场,磁感应强度大小为B1,在y轴左侧加方向垂直xoy平面向里的匀强磁场,电子在第(k+1)次从左向右经过y轴(经过P点为第1次)时恰好通过坐标原点。求y轴左侧磁场磁感应强度大小B2及从P点运动到坐标原点的时间t2
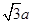 )点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为
)点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为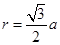 ,求:
,求:
(1)电子从坐标原点O 运动到P点的时间t1;
(2)所加圆形匀强磁场区域的最小面积;
(3)若电子到达y轴上P点时,撤去圆形匀强磁场,同时在y轴右侧加方向垂直xoy平面向里的匀强磁场,磁感应强度大小为B1,在y轴左侧加方向垂直xoy平面向里的匀强磁场,电子在第(k+1)次从左向右经过y轴(经过P点为第1次)时恰好通过坐标原点。求y轴左侧磁场磁感应强度大小B2及从P点运动到坐标原点的时间t2
(1)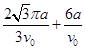 (2)
(2)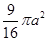 (3)
(3)
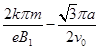
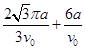 (2)
(2)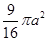 (3)
(3)
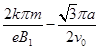
(1)由几何关系,电子从O点运动到P点的路程为:
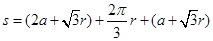
将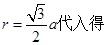
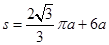
所以从O点运动到P点的时间为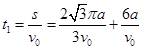
(2)以AB为直径的圆形磁场即为最小的圆形磁场区域,最小面积为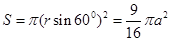
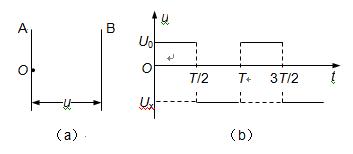
(3)设电子在y轴右侧和左侧做圆周运动的半径分别为r1和r2,则有
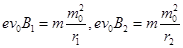
如图乙的几何关系可知
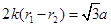
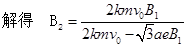
设电子在y轴右侧和左侧做圆周运动的周期分别为T1和T2, 则
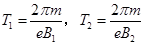

解得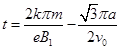
本题考查的是带电粒子在磁场中的运动问题,根据几何关系,应用带电粒子在磁场中的运动的相关公式,即可计算出结果;
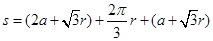
将
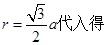
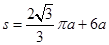
所以从O点运动到P点的时间为
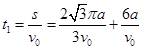
(2)以AB为直径的圆形磁场即为最小的圆形磁场区域,最小面积为
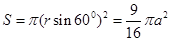
(3)设电子在y轴右侧和左侧做圆周运动的半径分别为r1和r2,则有
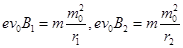
如图乙的几何关系可知

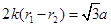
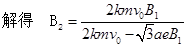
设电子在y轴右侧和左侧做圆周运动的周期分别为T1和T2, 则
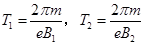

解得
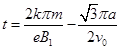
本题考查的是带电粒子在磁场中的运动问题,根据几何关系,应用带电粒子在磁场中的运动的相关公式,即可计算出结果;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目