题目内容
在动摩擦因数m=0.2的粗糙绝缘足够长的水平滑漕中,长为2L的绝缘轻质细杆两端各连接一个质量均为m的带电小球A和B,如图为俯视图(槽两侧光滑)。A球的电荷量为+2q,B球的电荷量为-3q(均可视为质点,也不考虑两者间相互作用的库仑力)。现让A处于如图所示的有界匀强电场区域MPQN内,已知虚线MP恰位于细杆的中垂线,MP和NQ的距离为3L,匀强电场的场强大小为E=1.2mg/q,方向水平向右。释放带电系统,让A、B从静止开始运动(忽略小球运动中所产生的磁场造成的影响)。求:
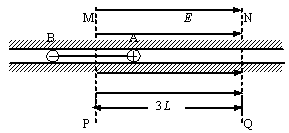
(1)小球B第一次到达电场边界MP所用的时间;
(2)小球A第一次离开电场边界NQ时的速度大小
(3)带电系统运动过程中,B球电势能增加量的最大值。

(1)小球B第一次到达电场边界MP所用的时间;
(2)小球A第一次离开电场边界NQ时的速度大小
(3)带电系统运动过程中,B球电势能增加量的最大值。
(1)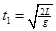 (2)
(2)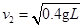 (3)x=0.1L
(3)x=0.1L
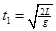 (2)
(2)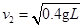 (3)x=0.1L
(3)x=0.1L(1)带电系统开始运动后,先向右加速运动;当B进入电场区时,开始做减速运动。设B进入电场前的过程中,系统的加速度为a1,
由牛顿第二定律:2Eq-m2mg=2ma1
即 a1=g (2分)
B刚进入电场时,由L=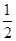 a1t12
a1t12
可得
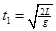 (2分)
(2分)
(2)当A刚滑到右边界时,电场力对系统做功为
W1=2Eq´2L+(—3Eq´L)=EqL
摩擦力对系统做功为W2=—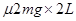 =—0.8mmgL
=—0.8mmgL
W总= EqL—0.8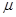 mgL="0.4" mgL
mgL="0.4" mgL
故A球从右端滑出。 (2分)。
设B从静止到刚进入电场的速度为v1,
由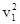 =2a1L
=2a1L
可得v1=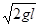 (2分)
(2分)
设B进入电场后,系统的加速度为a2,由牛顿第二定律
2Eq-3Eq-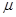 2mg=2ma2
2mg=2ma2
a2=-0.8g (2分)
系统做匀减速运动,设小球A第一次离开电场边界NQ时的速度大小为v2;
由 —
—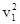 ="2" a2L (2分)
="2" a2L (2分)
可得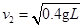 (2分)
(2分)
(3)当带电系统速度第一次为零,此时A已经到达右边界NQ外,B克服电场力做的功最多,B增加的电势能最多 (2分)
设此时A离右边界NQ的距离为x,由动能定理:
2Eq´2L— 3Eq´(L+x)—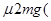 2L+x)=0 (2分)
2L+x)=0 (2分)
可得x=0.1L
所以B电势能增加的最大值 DW1=3Eq´1.1L=3.3EqL =3.96mgL (2分)
由牛顿第二定律:2Eq-m2mg=2ma1
即 a1=g (2分)
B刚进入电场时,由L=
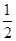 a1t12
a1t12 可得

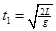 (2分)
(2分)(2)当A刚滑到右边界时,电场力对系统做功为
W1=2Eq´2L+(—3Eq´L)=EqL
摩擦力对系统做功为W2=—
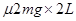 =—0.8mmgL
=—0.8mmgLW总= EqL—0.8
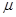 mgL="0.4" mgL
mgL="0.4" mgL 故A球从右端滑出。 (2分)。
设B从静止到刚进入电场的速度为v1,
由
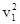 =2a1L
=2a1L 可得v1=
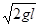 (2分)
(2分)设B进入电场后,系统的加速度为a2,由牛顿第二定律
2Eq-3Eq-
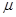 2mg=2ma2
2mg=2ma2 a2=-0.8g (2分)
系统做匀减速运动,设小球A第一次离开电场边界NQ时的速度大小为v2;
由
 —
—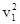 ="2" a2L (2分)
="2" a2L (2分)可得
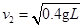 (2分)
(2分)(3)当带电系统速度第一次为零,此时A已经到达右边界NQ外,B克服电场力做的功最多,B增加的电势能最多 (2分)
设此时A离右边界NQ的距离为x,由动能定理:
2Eq´2L— 3Eq´(L+x)—
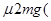 2L+x)=0 (2分)
2L+x)=0 (2分)可得x=0.1L
所以B电势能增加的最大值 DW1=3Eq´1.1L=3.3EqL =3.96mgL (2分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



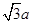 )点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为
)点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为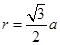 ,求:
,求:

 的匀强电场中,长为
的匀强电场中,长为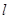 的绝缘轻杆可绕固定轴
的绝缘轻杆可绕固定轴 在竖直面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为
在竖直面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为 和
和 (
( ),A带负电,电量为
),A带负电,电量为 ,B带正电,电量为
,B带正电,电量为 。杆从静止开始由水平位置转到竖直位置,在此过程中电场力做功为 ,在竖直位置处两球的总动能为 。
。杆从静止开始由水平位置转到竖直位置,在此过程中电场力做功为 ,在竖直位置处两球的总动能为 。
 的带电微粒沿着竖直平面内的直线由A点运动到B点的过程中,微粒的( )
的带电微粒沿着竖直平面内的直线由A点运动到B点的过程中,微粒的( )
