Question

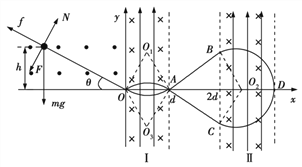
【题目】如图所示，直角坐标系xOy的第二象限存在垂直纸面向外的匀强磁场，磁感应强度大小为B1=1T，在0<x<d及x>2d的I、Ⅱ区域内存在竖直向上的匀强电场和垂直纸面向里的匀强电场，d=0.6m，电场强度大小均为E=2N/C,磁感应强度大小均为B2=T。一根绝缘粗糙的硬杆，下端位于坐标原点，倾角为θ=30°，一个质量为m=0.1kg、电荷量为q=0.5C的带正电小球中心有小孔，可穿在硬杆上，小球与硬杆间的动摩擦因素为=。将穿在硬杆上的小球从距离X轴高度为h=0.4m处由静止释放，小球经过O点之前已匀速，若小球进入磁场I、Ⅱ区域后能够返回O点，求：（重力加速度g=10m/s2）

（1）小球从开始运动到下滑到O点克服硬杆摩擦力做的功；

（2）Ⅱ区域磁场右边界的横坐标范围；

（3）小球从O点进入磁场I区域到再次返回O点经历的时间。

Answer 1

【答案】（1）（2）（3）

【解析】(1)小球在硬杆上匀速运动时，受重力、支持力、洛伦兹力、摩擦力作用，受力分析如图所示，由平衡条件可得

N=qvB1+mgcos θ

mgsin θ=f

f=μN

解得v=m/s

小球从开始运动到O点，由动能定理可得

mgh-W=mv2

解得W=0.38 J。

(2)如图所示，小球在磁场区域中运动，根据已知条件可知qE=mg，小球做匀速圆周运动，则

由qvB2=得，R=0.6 m

R=d，小球从Ⅰ区域边界离开，轨迹对应的圆心角为60°，从A点离开后再从B点进入Ⅱ区域，要使小球能返回原点，根据对称性作出运动轨迹如图所示，由几何关系可得小球在Ⅱ区域中轨迹对应的圆心角为240°，Ⅱ区域右边界到左边界的距离至少为x0=R+Rcos 60°

得x0=0.9 m

区域Ⅱ右边界的横坐标范围x>2d+x0=2.1 m。

(3)小球在Ⅰ和Ⅱ区域中运动周期均为T=

小球在Ⅰ区域运动时间为t1=×2

小球在无磁场区域运动时间t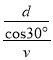2=×2

小球在区域Ⅱ中运动时间为t3=

小球从坐标原点进入磁场后到再次返回坐标原点经历的时间

t=t1+t2+t3

解得t=。