题目内容
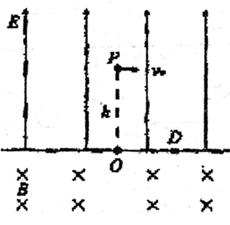
一宇宙人在太空(万有引力可以忽略不计)玩垒球.如图所示,辽阔的太空球场半侧为匀强电场,另半侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场方向与界面垂直,磁场方向垂直纸面向里,电场强度大小E=100V/m.宇宙人位于电场一侧距界面为h=3m的P点,O为P点至界面垂线的垂足,D点位于纸面上O点的右侧,OD与磁场的方向垂直.垒球的质量m=0.1kg,电量q=-0.05C.宇宙人从P点以初速度v1=10m/s平行于界面投出垒球,要使垒球第一次通过界面时就击中D点,求:(计算结果保留三位有效数字)
(1)O、D两点之间的距离.
(2)垒球从抛出到第一次回到P点的时间.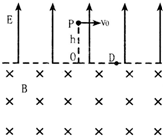
(1)O、D两点之间的距离.
(2)垒球从抛出到第一次回到P点的时间.

(1)设垒球在电场中运动的加速度大小为a,时间为t1,OD=d则:
a=
h=
at12
d=v1t
解得:a=50m/s2,t1=
s,d=2
m=3.46m
即O、D两点之间的距离为3.46m.
(2)垒球的运动轨迹如图所示.
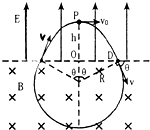
由图可知,tanθ=
=
,速度大小为:v=
=20m/s
设垒球作匀速圆周运动半径为R,磁感应强度大小为B,则R=
=4m
根据牛顿第二定律,有:qvB=m
解得B=
=10T
垒球在磁场中运动的时间为:t2=
×
=
s
垒球从抛出到第一次回到P点的时间为:t=2t1+t2=
s=1.53s;
a=
| qE |
| m |
h=
| 1 |
| 2 |
d=v1t
解得:a=50m/s2,t1=
| ||
| 5 |
| 3 |
即O、D两点之间的距离为3.46m.
(2)垒球的运动轨迹如图所示.

由图可知,tanθ=
| at1 |
| v1 |
| 3 |
| v1 |
| cosθ |
设垒球作匀速圆周运动半径为R,磁感应强度大小为B,则R=
| d |
| sinθ |
根据牛顿第二定律,有:qvB=m
| v2 |
| R |
解得B=
| mv |
| qR |
垒球在磁场中运动的时间为:t2=
| 360°-2×60° |
| 360° |
| 2πm |
| qB |
| 4π |
| 15 |
垒球从抛出到第一次回到P点的时间为:t=2t1+t2=
6
| ||
| 15 |

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
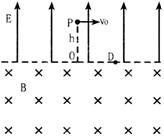
 (2008?安徽模拟)一宇宙人在太空(万有引力可以忽略不计)玩垒球.如图所示,辽阔的太空球场半侧为匀强电场,另半侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场方向与界面垂直,磁场方向垂直纸面向里,电场强度大小E=100V/m.宇宙人位于电场一侧距界面为h=3m的P点,O为P点至界面垂线的垂足,D点位于纸面上O点的右侧,OD与磁场的方向垂直.垒球的质量m=0.1kg,电量q=-0.05C.宇宙人从P点以初速度v1=10m/s平行于界面投出垒球,要使垒球第一次通过界面时就击中D点,求:(计算结果保留三位有效数字)
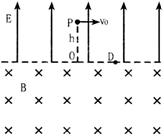
(2008?安徽模拟)一宇宙人在太空(万有引力可以忽略不计)玩垒球.如图所示,辽阔的太空球场半侧为匀强电场,另半侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场方向与界面垂直,磁场方向垂直纸面向里,电场强度大小E=100V/m.宇宙人位于电场一侧距界面为h=3m的P点,O为P点至界面垂线的垂足,D点位于纸面上O点的右侧,OD与磁场的方向垂直.垒球的质量m=0.1kg,电量q=-0.05C.宇宙人从P点以初速度v1=10m/s平行于界面投出垒球,要使垒球第一次通过界面时就击中D点,求:(计算结果保留三位有效数字)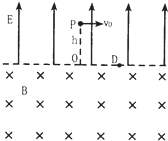 (2007?湖北模拟)一宇宙人在太空(万有引力可以忽略不计)玩垒球.如图所示,辽阔的太空球场半侧为匀强电场,另半侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场方向与界面垂直,磁场方向垂直纸面向里,电场强度大小 E=100V/m.宇宙人位于电场一侧距界面为 h=3m 的P点,O为P点至界面垂线的垂足,D点位于纸面上O点的右侧,OD与磁场的方向垂直.垒球的质量 m=0.1kg,电量 q=一0.05c.宇宙人从 P 点以初速度 v0=10m/s 平行于界面投出垒球,要使垒球第一次通过界面时就击中D点,求:(计算结果保留三位有效数字)
(2007?湖北模拟)一宇宙人在太空(万有引力可以忽略不计)玩垒球.如图所示,辽阔的太空球场半侧为匀强电场,另半侧为匀强磁场,电场和磁场的分界面为垂直纸面的平面,电场方向与界面垂直,磁场方向垂直纸面向里,电场强度大小 E=100V/m.宇宙人位于电场一侧距界面为 h=3m 的P点,O为P点至界面垂线的垂足,D点位于纸面上O点的右侧,OD与磁场的方向垂直.垒球的质量 m=0.1kg,电量 q=一0.05c.宇宙人从 P 点以初速度 v0=10m/s 平行于界面投出垒球,要使垒球第一次通过界面时就击中D点,求:(计算结果保留三位有效数字)