��Ŀ����
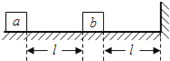
����Ŀ����ͼ1��ʾ,���ʵ���һ�˹̶�����ֱǽ����,��һ������һ����Ϊ0.10 kg��Сľ��a����ˮƽ�⻬������,����ҲΪ0.10 kg��Сľ��b����aһ���ھ�ֹ״̬������b��ʩ��һˮƽ�������Fʹa��b�Ӿ�ֹ��ʼ���������ƶ�����F�Ĵ�С��a��λ��x�Ĵ�С��ϵ��tu 2��ʾ����֪����ʼ�մ��ڵ������ڣ�����˵����ȷ����

A. ��ľ�������ƶ�10cm�Ĺ����У����ɵĵ������������� 2.5J
B. �õ��ɵľ���ϵ��Ϊ250 N/m
C. ��x = 10 cmʱ��ȥF,�˺�a��b����ʱ���ɵĵ�����Ϊ��
D. ��x= 10 cmʱ��ȥF, a��b����ʱA���ٶ�Ϊ![]() m/s
m/s
���𰸡�A
����������ľ�������ƶ�10cm�Ĺ����У�F����Ϊ �� ![]() ���ɹ��ܹ�ϵ�ɵã����ɵĵ�����������������F���Ĺ������Ե��ɵĵ�������������2.5J����A��ȷ����x=10cm=0.1mʱ�����ɵĵ���Ϊ F��=50N����F��==kx�� k=500N/m����B����x=10cmʱ��ȥF���˺�a��b����ʱ���ɵĵ���ӦΪ�㣬��C����x=10cm ʱ��ȥF��a��b����ʱ����֮��ĵ���Ϊ0�����ʱ���ߵļ��ٶ�Ϊa������ţ�ٵڶ����ɵã���a�� kx2=ma,��b�� 0=ma,��� x2=0,�ɹ��ܹ�ϵ��:
���ɹ��ܹ�ϵ�ɵã����ɵĵ�����������������F���Ĺ������Ե��ɵĵ�������������2.5J����A��ȷ����x=10cm=0.1mʱ�����ɵĵ���Ϊ F��=50N����F��==kx�� k=500N/m����B����x=10cmʱ��ȥF���˺�a��b����ʱ���ɵĵ���ӦΪ�㣬��C����x=10cm ʱ��ȥF��a��b����ʱ����֮��ĵ���Ϊ0�����ʱ���ߵļ��ٶ�Ϊa������ţ�ٵڶ����ɵã���a�� kx2=ma,��b�� 0=ma,��� x2=0,�ɹ��ܹ�ϵ��: ![]() ����� a��b����ʱ���ٶ�Ϊ
����� a��b����ʱ���ٶ�Ϊ ![]() ����D����������A��ȷ��BCD������
����D����������A��ȷ��BCD������

 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�