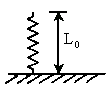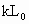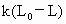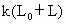题目内容
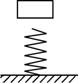
如图，一根弹簧竖直放置在地面上，上端为O点，某人将质量为m的物块放在弹簧上端O处，使它缓慢下落到A处，放手后物块处于平衡状态，在此过程中人做的功为W．如果将物块从距轻弹簧上端O点H高处释放，物块自由落下，落到弹簧上端O点后，继续下落将弹簧后压缩到A处时，物块速度V的大小为
|
|
分析：根据功能关系，求出弹簧的弹性势能；再由能量守恒定律，从而即可求解．
解答：解：将物块放在弹簧上端O处，并缓慢下落到A处，处于平衡状态，该过程重力势能的减少等于弹性势能的增加及克服人手对物块做的功，即
mghOA=W+Ep
从O点上方高H处释放，根据能量守恒定律有：
mg（H+hOA）=
mv2+Ep
解得v=
故答案为：
mghOA=W+Ep
从O点上方高H处释放，根据能量守恒定律有：
mg（H+hOA）=
| 1 |
| 2 |
解得v=
|
故答案为：
|
点评：考查功能关系的应用，掌握能量守恒定律．注意过程中功的正负，当然也可用动能定理来解题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
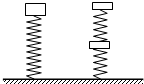（2009?孝感模拟）如图所示，一根轻质弹簧竖直放在桌面上，下端固定，上端放一重物m，稳定后弹簧长为L；现将弹簧截成等长的两段，将重物分成两块，如图所示连接后，稳定时两段弹簧的总长为L′，则（ ）
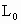，劲度系数为k是的轻弹簧，竖直固定在水平地面上，在其上面放上一重物后，弹簧的长度变为L，此时弹簧的弹力大小为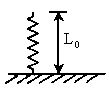
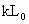
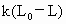
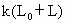
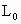，劲度系数为k是的轻弹簧，竖直固定在水平地面上，在其上面放上一重物后，弹簧的长度变为L，此时弹簧的弹力大小为
