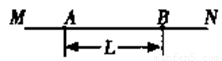题目内容
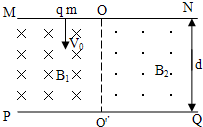
如图所示，在直线MN与PQ之间有两个匀强磁场区域，两磁场的磁感应强度分别为B
l、B
2，方向均与纸面垂直，两磁场的分界线OO'与MN和PQ都垂直．现有一带正电的粒子质量为m、电荷量为q，以速度V
0垂直边界MN射入磁场B
l，并最终垂直于边界PQ从O'Q段射出，已知粒子始终在纸面内运动，且每次均垂直OO'越过磁场分界线．
（1）写出MN与PQ间的距离d的表达式．
（2）用d、V
0表示粒子在磁场中运动的时间．
分析：（1）粒子在O′Q间射出，画出轨迹，根据洛伦兹力提供向心力求出在两个磁场中的运动半径，根据几何关系即可求出d的表达式；
（2）求出粒子在两个磁场中运动的周期，粒子在O'Q间射出，在两个磁场中分别经历2n十1个
，进而求出时间．
解答：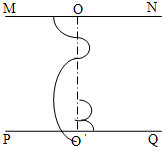
解：（1）粒子在O′Q间射出，轨迹如图所示．
由 qv
0B=m
得R
1=
，
同理得 R
2=
又d=（2n+1）（R
1+R
2）（n=0，1，2，3…）
因此d=
V0（n=0，1，2，3…）
（2）粒子在磁场B
1中做圆周运动的周期
T1=，
在磁场B
2中做圆周运动的周期
T2=粒子在O'Q间射出，在两个磁场中分别经历2n十1个
，则
| | t=(2n+1)×(+) | | =(2n+1)××(+) | | = |
| |
答：（1）MN与PQ间的距离d的表达式为d=
V0（n=0，1，2，3…）．
（2）粒子在磁场中运动的时间为
．
点评：本题主要考查了带电粒子在磁场中运动的问题，要求同学们能画出运动轨迹，能求出半径及周期，难度适中．
练习册系列答案
相关题目
出彩同步大试卷系列答案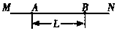
（2006?潍坊一模）如图所示，在直线MN上有一个点电荷，A、B是直线MN上的两点，两点的间距为L，场强大小分别为E和2E．则（ ）
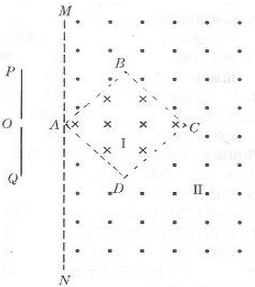（2008?湛江二模）如图所示，在直线MN右侧正方形ABCD区域内、外分布着方向相反且与平面垂直的匀强磁场Ⅰ和Ⅱ，磁感应强度的大小都为B．正方形边长为L，AB边与直线MN方向夹角为45°．现有一质量为m、电荷量为q的带负电的微粒通过小孔O进入PQ与MN间的加速电场区域（进入时可认为初速度为零），微粒经电场加速后从正方形ABCD区域内的A点进入磁场，微粒进入磁场的速度垂直MN，也垂直于磁场．不计微粒的重力．
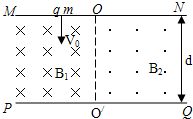如图所示，在直线MN与PQ之间有两个匀强磁场区域，两磁场的磁感应强度分别为Bl、B2，方向均与纸面垂直，两磁场的分界线OO′与MN和PQ都垂直．现有一带正电的粒子质量为m、电荷量为q，以速度v0垂直边界MN射入磁场Bl，并最终垂直于边界PQ从O'Q段射出，已知粒子始终在纸面内运动，且每次均垂直OO'越过磁场分界线．