题目内容
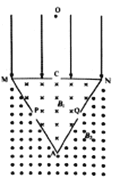
【题目】如图所示，三块挡板围成截面边长L＝1.2m的等边三角形区域，C、P、Q分别是MN、AM和AN中点处的小孔，三个小孔处于同一竖直面内，MN水平，MN上方是竖直向下的匀强电场，场强E=4×10-4N /C。三角形区域内有垂直纸面向里的匀强磁场，磁感应强度为B1；AMN以外区域有垂直纸面向外， 磁感应强度大小为B2＝3B1的匀强磁场。现将一比荷q/m=108C/kg的帯正电的粒子，从O点由静止释放，粒子从MN小孔C进入内部匀强磁场，经内部磁场偏转后直接垂直AN经过Q点进入外部磁场。已知粒子最终回到了O点，OC相距2m。设粒子与挡板碰撞过程中没有动能损失，且电荷量不变，不计粒子重力，不计挡板厚度，取π＝3。求：
（1）磁感应强度B1的大小；
（2）粒子从O点出发，到再次回到O点经历的时间；
（3）若仅改变B2的大小，当B2满足什么条件时，粒子可以垂直于MA经孔P回到O点（若粒子经过A点立即被吸收）。
【答案】（1）
（2）
（3）
【解析】
（1）粒子从O到C即为在电场中加速，则由动能定理得：
解得v=400 m/s
带电粒子在磁场中运动轨迹如图所示。
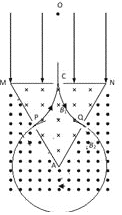
由几何关系可知
由
代入数据得
（2）由题可知B2=3B1=2×10-5T
则
由运动轨迹可知：进入电场阶段做匀加速运动，则
得到t1=0.01s
粒子在磁场B1中的周期为
则在磁场B1中的运动时间为
在磁场B2中的运动周期为
在磁场B2中的运动时间为
则粒子在复合场中总时间为：
（3）设挡板外磁场变为
，粒子在磁场中的轨迹半径为r，则有
根据已知条件分析知，粒子可以垂直于MA经孔P回到O点，需满足条件
，其中k=0、1、2、3……
解得
练习册系列答案
相关题目
