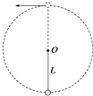
[题目]月球环绕地球运动的轨道半径约为地球半径的60倍.其运行周期约为27天．现应用开普勒定律计算:在赤道平面内离地面多高时.人造地球卫星可随地球一起转动.就像其停留在天空中不动一样．若两颗人造卫星绕地球做圆周运动.周期之比为1∶8.则它们轨道半径之比是多少?(已知R地＝6.4×103 km) 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】月球环绕地球运动的轨道半径约为地球半径的60倍，其运行周期约为27天．现应用开普勒定律计算：在赤道平面内离地面多高时，人造地球卫星可随地球一起转动，就像其停留在天空中不动一样．若两颗人造卫星绕地球做圆周运动，周期之比为1∶8，则它们轨道半径之比是多少？(已知R地＝6.4×103 km)

【答案】3.63×104 km　1∶4

【解析】月球和人造地球卫星都在环绕地球运转，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．设人造地球卫星运动的半径为R，周期为T＝1天，根据开普勒第三定律有：＝k，同理设月球轨道半径为R′，周期为T′，也有＝k

由以上两式可得＝

R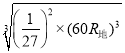＝＝＝6.67R地

在赤道平面内离地面高度

H＝R－R地＝6.67R地－R地＝5.67R地

＝5.67×6.4×103 km＝3.63×104 km.

由开普勒第三定律：＝

又因为T1∶T2＝1∶8，解得R1∶R2＝1∶4.

练习册系列答案

A. 力F所做功减去克服阻力所做的功等于重力势能的增量

B. 木箱克服重力所做的功等于重力势能的增量

C. 力F、重力、阻力，三者合力所做的功等于木箱动能的增量

D. 力F和阻力的合力所做的功等于木箱机械能的增量

【题目】如图为远距离输电示意图，发电机的输出电压U1和输电线的电阻和理想变压器匝数均不变，且n1：n2=n4：n3，当用户消耗的功率增大时，下列表述正确的是（　　）

A. 用户的总电阻增大

B. 用户两端的电压U4减小

C. U1：U2=U4：U3

D. 用户端增加的功率等于升压变压器多输入的功率

【题目】在“探究平抛运动规律”的实验中：

①在做“研究平抛运动”的实验时，让小球多次沿同一轨道运动，通过描点法画小球做平抛运动的轨迹．为了能较准确地描绘运动轨迹，

A．通过调节使斜槽的末端保持

B．每次释放小球的位置必须（填“相同”或者“不同”）

C．每次必须由释放小球（“运动”或者“静止”）

D．小球运动时不应与木板上的白纸相接触

E．将球的位置记录在纸上后，取下纸，将点连成（“折线”或“直线”或“光滑曲线”）

②某同学在做“研究平抛物体的运动”的实验中，忘记记下小球抛出点的位置O，如图所示，A为物体运动一段时间后的位置。g取10m/s2，根据图象，可知平抛物体的初速度为；小球抛出点的位置O的坐标为。

【题目】某同学在用油膜法估测分子直径的实验中：

（1）他将1滴配置好的油酸溶液滴入盛水的浅盘中，让油膜在水面上尽可能散开，待液面稳定后，在水面上形成油酸的_____油膜；把带有方格的玻璃板放在浅盘上，在玻璃板上描绘出油膜的边界轮廓，形状如图所示。已知坐标方格边长L=1 cm，按要求数出油膜轮廓线包括的方格是n=60个，则油酸的面积S约为_____ cm2；

（2）在用公式d=V/S计算油膜分子大小时，式中V的物理意义是_____。

A．指1 mL的油酸溶液的体积 B．指一滴油酸溶液的体积

C．指一滴油酸溶液中所含纯油酸的体积 D．指一滴油酸溶液中酒精的体积

（3）已知油酸溶液的配置比为0.025%，100滴油酸溶液的体积为1 mL，由以上数据估测出油酸分子的直径约为_____m。（保留2位有效数字）

【题目】如图所示，一根长为0.1 m的细线，一端系着一个质量是0.18kg的小球，拉住线的另一端，使球在光滑的水平桌面上做匀速圆周运动，当小球的转速增加到原转速的3倍时，细线断裂，这时测得线的拉力比原来大40 N．求：

（1）线断裂的瞬间，线的拉力；

（2）这时小球运动的线速度；

（3）如果桌面高出地面0.8 m，线断裂后小球沿垂直于桌子边缘的方向水平飞出去落在离桌面的水平距离．

【题目】如图所示，质量的足够长的木板放置在水平面上，质量的物块可视为质点放置在木板上，距高木板右端的距离，已知木板与地面之间的动摩擦因数，物块与木板之间的动摩擦因数，木板的右端与墙壁的距离，先给木板和木块一个向右的共同的初速度，木板右端有一层黏性物质，当木板与墙壁发生碰撞的瞬间，木板的速度减为零并粘在墙上,物块与墙壁发生的是弹性碰撞。g取，求：