题目内容
18. 如图所示,A、B是一对平行的金属板,在两板间加有一周期为T的交变电压u,A板的电势φA=0,B板的电势φB随时间的变化规律为:在0到$\frac{T}{2}$的时间内,φB=φ0(φ0为正的常数);在$\frac{T}{2}$到T的时间内,φB=-φ0;在T到$\frac{3T}{2}$的时间内,φB=φ0;在$\frac{3T}{2}$到2T的时间内,φB=-φ0…,现有一电子在t时刻从A极板附近由静止释放,不计重力,则下列判断错误的是( )
如图所示,A、B是一对平行的金属板,在两板间加有一周期为T的交变电压u,A板的电势φA=0,B板的电势φB随时间的变化规律为:在0到$\frac{T}{2}$的时间内,φB=φ0(φ0为正的常数);在$\frac{T}{2}$到T的时间内,φB=-φ0;在T到$\frac{3T}{2}$的时间内,φB=φ0;在$\frac{3T}{2}$到2T的时间内,φB=-φ0…,现有一电子在t时刻从A极板附近由静止释放,不计重力,则下列判断错误的是( )| A. | 若t=0,则电子将一直向B板运动,最后打在B板上 | |
| B. | 若t=$\frac{3T}{8}$,则电子一定会打在B板上 | |
| C. | 若t=$\frac{T}{8}$,则电子一定会打在B板上 | |
| D. | 若t=$\frac{T}{4}$,则电子可能在A、B两极板间往复运动 |
分析 分析电子的受力情况,来确定电子的运动情况,如果电子一直向上运动,一定能到达B板;如果时而向B板运动,时而向A板运动,则通过比较两个方向的位移大小,分析能否到达B板.
解答 解:A、电子在t=0时刻进入时,在一个周期内,前半个周期受到的电场力向上,向上做加速运动,后半个周期受到的电场力向下,继续向上做减速运动,T时刻速度为零,接着周而复始,所以电子一直向B板运动,一定会打在B板上.故A正确;
B、若电子是在t=$\frac{3T}{8}$刻进入的,在$\frac{3}{8}$T~$\frac{1}{2}$,向上加速;$\frac{1}{2}$~$\frac{5}{8}$T,向上减速;$\frac{5}{8}$T~T,向下加速;T~$\frac{11}{8}$,向下减速,速度减小为零,完成一个周期的运动,接着周而复始,所以电子时而向B板运动,时而向A板运动,根据运动学规律可知,在一个周期内电子向B板运动的位移小于向A板运动的位移,所以电子最后一定不会打在B板上,而是从A板返回;故B错误;
C、若电子是在t=$\frac{T}{8}$时刻进入时,在一个周期内:在 $\frac{T}{8}$~$\frac{T}{2}$,电子受到的电场力向上,向B板做加速运动,在$\frac{1}{2}$T~$\frac{7}{8}$T内,受到的电场力向下,继续向B板做减速运动,$\frac{7}{8}$T时刻速度为零,$\frac{7}{8}$T~T接着向A板运动,T~$\frac{9}{8}$T时间内继续向A板运动,$\frac{9}{8}$T时刻速度为零,完成一个周期的运动,接着周而复始,所以电子时而向B板运动,时而向A板运动,根据运动学规律可知,在一个周期内电子向B板运动的位移大于向A板运动的位移,所以电子最后一定会打在B板上.故C正确;
C、若电子是在t=$\frac{T}{4}$时刻进入的,在$\frac{T}{4}$~$\frac{T}{2}$阶段是向上加速;在$\frac{1}{2}$T~$\frac{3}{4}$T向上减速,末速度为零;在$\frac{3}{4}$T~T反向加速,T~$\frac{5}{4}$T反向减速,末速度为零,完成一个周期的运动,接着周而复始,所以电子时而向B板运动,时而向A板运动,以某一点为中心做往复运动,故D正确;
本题选错误的,故选:B.
点评 因极板间加交变电场,故粒子的受力是周期性变化的,本题应通过受力情况先确定粒子的运动情况.根据位移情况判断电子能否打在B板上.

 53随堂测系列答案
53随堂测系列答案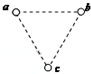 如图,在光滑绝缘水平面上,三个带电质点a、b和c分别位于边长为L的正三角形的三个顶点上;a、b电荷量均为q且为同种电荷,整个系统置于水平方向的匀强电场中.已知静电力常量为k,若三个质点均处于静止状态,则下列说法正确的是( )
如图,在光滑绝缘水平面上,三个带电质点a、b和c分别位于边长为L的正三角形的三个顶点上;a、b电荷量均为q且为同种电荷,整个系统置于水平方向的匀强电场中.已知静电力常量为k,若三个质点均处于静止状态,则下列说法正确的是( )| A. | 如果a、b带正电,那么c一定带负电 | B. | 匀强电场场强的大小为$\frac{\sqrt{3}kq}{{l}^{2}}$ | ||
| C. | 质点c的电量大小为$\sqrt{2}$q | D. | 匀强电场的方向与ab边垂直背离c |
| A. | 竖直上抛的物体 | B. | 水平抛出的物体 | C. | 自由下落的物体 | D. | 匀速升降的物体 |
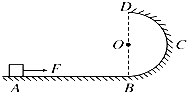 如图10所示,水平轨道AB与位于竖直面内半径为R=0.90 m的半圆形光滑轨道BCD相连,半圆形轨道的BD连线与AB垂直.质量为m=1.0kg可看做质点的小滑块在恒定外力F作用下从水平轨道上的A点由静止开始向右运动,滑块与水平轨道AB间的动摩擦因数 μ=0.5.到达水平轨道的末端B点时撤去外力,滑块继续沿半圆形轨道运动,且恰好能通过轨道最高点D,滑块脱离半圆形轨道后又刚好落到A点.g取10m/s2,求:
如图10所示,水平轨道AB与位于竖直面内半径为R=0.90 m的半圆形光滑轨道BCD相连,半圆形轨道的BD连线与AB垂直.质量为m=1.0kg可看做质点的小滑块在恒定外力F作用下从水平轨道上的A点由静止开始向右运动,滑块与水平轨道AB间的动摩擦因数 μ=0.5.到达水平轨道的末端B点时撤去外力,滑块继续沿半圆形轨道运动,且恰好能通过轨道最高点D,滑块脱离半圆形轨道后又刚好落到A点.g取10m/s2,求: 在“用油膜法估测油酸分子的大小”实验中,将1cm3的油酸溶于酒精,制成300cm3的油酸酒精溶液,测得1cm3的油酸酒精溶液有100滴,现取一滴该油酸酒精溶液滴在水面上,最后形成的油酸膜形状和尺寸如图所示,坐标中正方形小方格的边长为1cm,则由此估算出油酸分子的直径为多少米?(结果保留一位有效数字)
在“用油膜法估测油酸分子的大小”实验中,将1cm3的油酸溶于酒精,制成300cm3的油酸酒精溶液,测得1cm3的油酸酒精溶液有100滴,现取一滴该油酸酒精溶液滴在水面上,最后形成的油酸膜形状和尺寸如图所示,坐标中正方形小方格的边长为1cm,则由此估算出油酸分子的直径为多少米?(结果保留一位有效数字)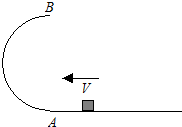 在竖直平面内有一半径为R的光滑半圆形固定轨道,其最低点A和水平面相切.一质量为m的物块从最低点以某一速度冲上轨道,到达最高点B时和半圆轨道之间的作用力的大小为mg,求:
在竖直平面内有一半径为R的光滑半圆形固定轨道,其最低点A和水平面相切.一质量为m的物块从最低点以某一速度冲上轨道,到达最高点B时和半圆轨道之间的作用力的大小为mg,求: