Question

【题目】如图所示，在轴上方存在垂直于平面向外的匀强磁场，坐标原点处有一粒子源，可向轴和轴上方的平面各个方向不断地发射质量为、带电量为、速度大小均为的粒子。在轴上距离原点处垂直于轴放置一个长度为、厚度不计、两侧均能接收粒子的薄金属板（粒子打在金属板上即被吸收，电势保持为0）。沿轴负方向射出的粒子恰好打在薄金属板的上端，不计带电粒子的重力和粒子间相互作用力。

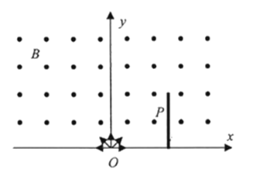
（1）求磁感应强度的大小；

（2）求被薄金属板接收的粒子在磁场运动的最短时间与最长时间；

（3）要使薄金属板右侧不能接收到粒子，求挡板沿轴正方向移动的最小距离。

Answer 1

【答案】（1）（2）；（3）

【解析】

（1）设粒子做圆周运动的半径为。

根据牛顿第二定律，得：

由几何关系，得：

联立解得：；

（2）带电粒子在磁场中的运动周期为，则有：，

得

打在左侧下端的粒子在磁场中运动的时间最短；

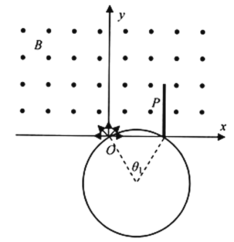
由几何关系可知：打在左侧下端的粒子在磁场中偏转的角度是

运动的最短时间：

联立解得：

打在右侧下端的粒子在磁场中运动的时间最长，

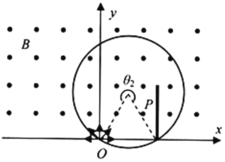
由几何关系可知：打在左侧下端的粒子在磁场中偏转的角度是，

运动的最短时间：

联立解得：

（3）带电粒子能达到的范围如图阴影所示:

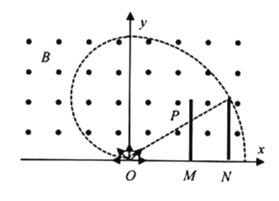
要使挡板右侧无粒子到达，板最上端与点的连线长应为即粒子运动的直径.

所以沿轴正方移动的最小长度.

，