��Ŀ����
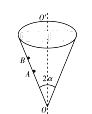
����Ŀ����ѧ����Ϊ��̫��ϵ�г����������п��ܳ�����������������---̩̹��Ϊ���о����������������Ƿ���һ������Ϊm��̽������ʹ̽��������������������ʱ���ܹ���������������Բ���˶�����ʱ̽������������������ĸ߶�Ϊh���Ժ�̽�������Ծ���һϵ�е��ƶ��������������渽����Ȼ��ʼ�Գ��ٶ�![]() ��ֱ�����������ȼ������䣬ֱ����ͣ�����õ�ʱ��Ϊt������켣Ϊֱ�ߡ��������İ뾶ΪR��������������������ٶ�Ϊg����������ΪG����
��ֱ�����������ȼ������䣬ֱ����ͣ�����õ�ʱ��Ϊt������켣Ϊֱ�ߡ��������İ뾶ΪR��������������������ٶ�Ϊg����������ΪG����
(1)̽��������������Բ���˶������ڣ�
(2)�������ĵ�һ�����ٶȼ�ƽ���ܶȣ�
(3)̽��������ʱ��������ƽ������F��
���𰸡�(1) ![]() ��(2)
��(2) ![]() ��(3)F=m(
��(3)F=m(![]() +g)��
+g)��
���������������������������������������ţ�ٵڶ����ɼ���������ڣ�����ţ�ٵڶ���������������ٽ���ܶȹ�ʽ��������ܶȣ������ȱ���ֱ���˶����ɣ�̽��������ʱ�ļ��ٶȣ�����ţ�ٵڶ��������������
(1)��������������壬��������������������![]()
����̽��������![]()
�������: ![]()
(2)̽�����������������������������ṩ����: ![]()
���������ĵ�һ�����ٶ�![]()
���Ͽ�֪![]() ��
��![]()
��������������ƽ���ܶ�: ![]()
(3)�����ȱ���ֱ���˶����ɣ�̽��������ʱ�ļ��ٶ�Ϊ![]()
����ţ�ٵڶ���������F-mg=ma
�����![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�