题目内容
12.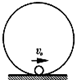 如图所示,半径r=0.5m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一小球(小球的半径比r小很多).现给小球一个水平向右的初速度v0,要使小球不脱离轨道运动,重力加速度g取10m/s2,则下列初速度v0范围能满足的是( )
如图所示,半径r=0.5m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一小球(小球的半径比r小很多).现给小球一个水平向右的初速度v0,要使小球不脱离轨道运动,重力加速度g取10m/s2,则下列初速度v0范围能满足的是( )| A. | v0≥5m/s | B. | v0≥2$\sqrt{5}$m/s | C. | v0≥$\sqrt{5}$m/s | D. | v0≤$\sqrt{10}$m/s |
分析 要使小球不脱离轨道运动,1、越过最高点.2、不越过四分之一圆周.根据动能定理求出初速度v0的条件
解答 解:最高点的临界情况:mg=$m\frac{{v}^{2}}{r}$,
解得:v=$\sqrt{gr}$
根据动能定理得:-mg•2r=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$
解得:v0=5m/s.
若不通过四分之一圆周,根据动能定理有:
-mgr=0-$\frac{1}{2}m{{v}_{0}}^{2}$
解得:v0=$\sqrt{10}$m/s.
所以初速度v0范围为v0≥5m/s或v0≤$\sqrt{10}$m/s.故AD正确,B、C错误.
故选:AD
点评 解决本题的关键知道小球在内轨道运动最高点的临界情况,以及能够熟练运用动能定理,难度不大,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
3.下列单位中属于国际单位制(SI)基本单位的是( )
| A. | 千克 | B. | 千米 | C. | 千焦 | D. | 千帕 |
7.如图所示,A、B是完全相同的两个小灯泡,L为自感系数很大、电阻可以忽略的带铁芯的线圈,则( )
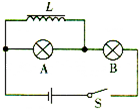

| A. | 开关S闭合瞬间,B灯亮,A灯不亮 | |
| B. | 开关S闭合瞬间,A、B同时发光,随后A灯变暗直至熄灭,B灯变亮 | |
| C. | 断开开关S的瞬间,A、B灯同时熄灭 | |
| D. | 断开开关S的瞬间,B灯立即熄灭,A灯突然闪亮一下再熄灭 |
1.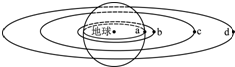 四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )
四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )
 四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )
四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )| A. | c相对于b静止 | B. | 相同时间内b转过的弧长最长 | ||
| C. | a的向心加速度最大 | D. | d的运行周期可能是23 h |
2.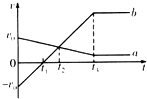 带同种电荷的a、b两小球在光滑水平上相向运动.已知当小球间距小于或等于L时,两者间的库仑力始终相等;小球间距大于L时,库仑力为零.两小球运动时始终未接触,运动时速度v随时间t的变化关系图象如图所示.由图可知( )
带同种电荷的a、b两小球在光滑水平上相向运动.已知当小球间距小于或等于L时,两者间的库仑力始终相等;小球间距大于L时,库仑力为零.两小球运动时始终未接触,运动时速度v随时间t的变化关系图象如图所示.由图可知( )
 带同种电荷的a、b两小球在光滑水平上相向运动.已知当小球间距小于或等于L时,两者间的库仑力始终相等;小球间距大于L时,库仑力为零.两小球运动时始终未接触,运动时速度v随时间t的变化关系图象如图所示.由图可知( )
带同种电荷的a、b两小球在光滑水平上相向运动.已知当小球间距小于或等于L时,两者间的库仑力始终相等;小球间距大于L时,库仑力为零.两小球运动时始终未接触,运动时速度v随时间t的变化关系图象如图所示.由图可知( )| A. | a小球质量大于b小球质量 | |
| B. | 在t2时刻两小球间距最大 | |
| C. | 在0~t3时间内两小球间距逐渐减小 | |
| D. | 在0~t2时间内b小球所受斥力方向始终与运动方向相反 |
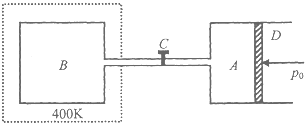 如图所示,水平放置的气缸A和容积为VB=3.6L的容器B,由一容积可忽略不计的长细管经阀门C相连,气缸A内有一活塞D,它可以无摩擦地在气缸内滑动,A放在温度恒为T1=300K,压强为p0=1.0×105Pa的大气中,B浸在T2=400K的恒温槽内,B的器壁导热性能良好,开始时C是关闭的,A内装有温度为T1=300K,体积为VA=2.4L的气体,B内没有气体,打开阀门C,使气体由A流入B,等到活塞D停止移动一段时间后,求以下两种情况下气体的体积和压强.
如图所示,水平放置的气缸A和容积为VB=3.6L的容器B,由一容积可忽略不计的长细管经阀门C相连,气缸A内有一活塞D,它可以无摩擦地在气缸内滑动,A放在温度恒为T1=300K,压强为p0=1.0×105Pa的大气中,B浸在T2=400K的恒温槽内,B的器壁导热性能良好,开始时C是关闭的,A内装有温度为T1=300K,体积为VA=2.4L的气体,B内没有气体,打开阀门C,使气体由A流入B,等到活塞D停止移动一段时间后,求以下两种情况下气体的体积和压强.
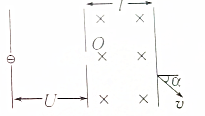 如图所示,初速度可忽略不计的电子经加速电场加速后从小孔O进入磁感应强度为B的有界磁场,磁场宽度为l,射出磁场时电子的偏转角为α,已知加速电场电势差为U,求电子的比荷.
如图所示,初速度可忽略不计的电子经加速电场加速后从小孔O进入磁感应强度为B的有界磁场,磁场宽度为l,射出磁场时电子的偏转角为α,已知加速电场电势差为U,求电子的比荷.