题目内容
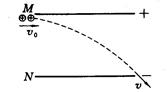
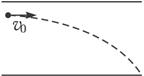
(14分)如图所示,在平面内水平和竖直的虚线L1、L2将平面分为四个区域,L2的左侧有一随时间变化的匀强电场,电场的变化情况如图所示(图象中场强大小E0为已知量,其他量均为未知),电场强度方向与L1平行且水平向右。L2的右侧为匀强磁场,方向垂直纸面向外。现将一绝缘挡板放在第一个区域内,其与L1、L2的交点M、N到O点的距离均为2b。在图中距L1为b、L2为4b的A点有一粒子源,可以发射质量为m,电荷量为+q的粒子(粒子的初速度近似为零,不计重力),粒子与挡板碰后电荷量不变,速度大小不变,方向变为平行于L2,当粒子第一次到达理想边界L2时电场消失,粒子再次与挡板碰撞的同时匀强电场恢复且粒子源发射下一个粒子,如此重复。


(1)求粒子第一次到达边界L2时的速度大小及速度方向与虚线L1的夹角;
(2)若粒子源在t=0时刻发射一粒子,粒子进入右面磁感应强度为B0的匀强磁场中,恰好打在挡板M处。求坐标轴中的T1、T2的值分别是多少?


(1)求粒子第一次到达边界L2时的速度大小及速度方向与虚线L1的夹角;
(2)若粒子源在t=0时刻发射一粒子,粒子进入右面磁感应强度为B0的匀强磁场中,恰好打在挡板M处。求坐标轴中的T1、T2的值分别是多少?
(1)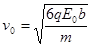
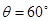 (2)
(2)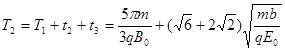
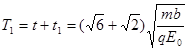
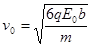
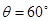 (2)
(2)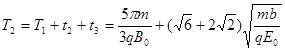
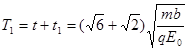
试题分析:(1)方法一:设粒子与板作用前的瞬间,速率为v0,由动能定理有
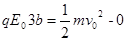 ........2分(这个方程也可以用下面两个方程代替
........2分(这个方程也可以用下面两个方程代替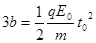 ,
,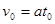 ,每个方程1分;或写作
,每个方程1分;或写作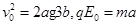 每个方程1分)
每个方程1分)得
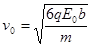
粒子与挡板碰后在电场中做类平抛运动
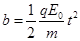 ........2分(其中只列出
........2分(其中只列出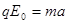 给1分)
给1分) 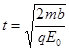
粒子到达L2时垂直于L2的速度大小
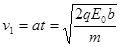 ........1分(方程也可写作
........1分(方程也可写作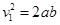 )
)粒子到达L2时的速度大小为
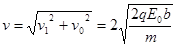 ........1分
........1分粒子第一次达到L2的速度与L1方向的夹角
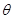
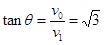 ........1分
........1分 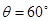 ........1分
........1分方法二: 根据动能定理
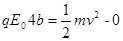 ........3分
........3分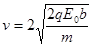 ........1分
........1分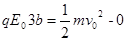 ........2分(这个方程也可以用下面两个方程代替
........2分(这个方程也可以用下面两个方程代替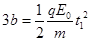 ,
,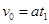 ,每个方程1分;或写作
,每个方程1分;或写作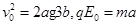 每个方程1分)
每个方程1分)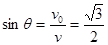 ........1分
........1分 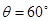 ........1分
........1分方法三: 根据动能定理
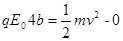 ........3分
........3分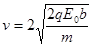 ........1分
........1分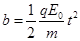 ........1分(
........1分(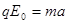 ,给1分)
,给1分) 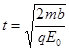
粒子到达L2时垂直于L2的速度大小
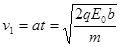 ........1分(方程也可写作
........1分(方程也可写作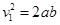 )
)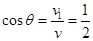
 ........1分
........1分 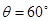 ........1分
........1分(2)粒子碰到挡板前的时间
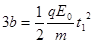 ........1分 (无论前面采用什么方法做的,这一问中只要体现出时间t1和t就给1分)
........1分 (无论前面采用什么方法做的,这一问中只要体现出时间t1和t就给1分) 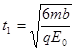
则坐标轴中的
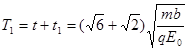 ........1分
........1分粒子在磁场中运动的时间
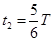 ......1分
......1分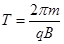 ......1分
......1分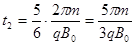
粒子由C点运动到M点的时间
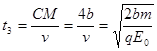 ...(只看方程)1分
...(只看方程)1分则坐标轴中的
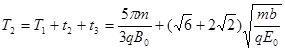 ........1分
........1分点评:带电粒子在电场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程(平衡、加速、减速,直线或曲线),然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化的观点,选用动能定理和功能关系求解.带电粒子在磁场中运动时,需要先画出粒子的运动轨迹,然后结合几何知识分析解题,

练习册系列答案
相关题目

 时间内,电场力对粒子做功为
时间内,电场力对粒子做功为

 和后
和后

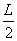
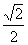 L
L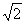 L
L
