��Ŀ����
6��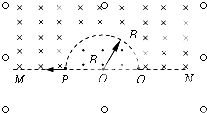 ��ͼ��ʾ��ֱ��MN�·��ų����Ϸ��ռ����������ǿ�ų�����ֽ����ǰ뾶ΪR�İ�Բ������Ĵų������෴�Ҵ�ֱ��ֽ�棬�Ÿ�Ӧǿ�ȴ�С��ΪB������һ����Ϊm�������Ϊq�Ĵ���������P���ذ뾶�����������������մ�Q�㣬����������������
��ͼ��ʾ��ֱ��MN�·��ų����Ϸ��ռ����������ǿ�ų�����ֽ����ǰ뾶ΪR�İ�Բ������Ĵų������෴�Ҵ�ֱ��ֽ�棬�Ÿ�Ӧǿ�ȴ�С��ΪB������һ����Ϊm�������Ϊq�Ĵ���������P���ذ뾶�����������������մ�Q�㣬������������������1�����ڴų����˶������ڣ�
��2����P�㾭���߽�һ�ε�Q�㣬�����˶��ٶȴ�С���˶�ʱ�䣻
��3��������ų����н�ģ��ֲ�����O��ΪԲ�ġ��뾶ΪR��2R������Բ֮��������������Դ�P���ذ뾶���������������������ܵ���Q�㣬�����ٶȵ����ֵ��
���� ��1�������ڴų�����Բ���˶�����ţ�ٵڶ�����������ӵ��ٶȣ�Ȼ��������ڣ�
��2�������ٶ����ʱ���ӵ��˶��켣��Ȼ��������ӵĹ���뾶����������ӵ��ٶ����˶�ʱ�䣮
��3�����������������ӿ��ܵ��˶��켣����ţ�ٵڶ���������ѧ֪ʶ�����ó������˶��Ŀ��ܵ������Ȼ���ɼ���֪ʶ�����켣�뾶�����ֵ���ɰ뾶��ʽ����ٶȵ����ֵ��
��� �⣺��1�������ڴų�����Բ���˶������������ṩ��������
��ţ�ٵڶ����ɵã�$B{v_0}q=m\frac{v_0^2}{r}$�����ڣ�$T=\frac{2��r}{v_0}$�������ڣ�$T=\frac{2��m}{Bq}$��
��2��������Բ���˶��Ĺ���뾶��r=$\frac{mv}{qB}$�������ٶ�Խ�����ӹ���뾶Խ��
�����ٶ����ʱ����P�㾭���߽�һ�ε�Q�㣬���ӵ��˶��켣��ͼ��ʾ��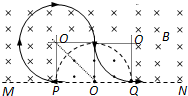
�ɼ���֪ʶ��֪�����ӹ���뾶��r=R��
��ţ�ٵڶ����ɵã�qvB=m$\frac{{v}^{2}}{r}$��
��ã���������ٶȣ�v=$\frac{qBR}{m}$��
������Բ���˶������ڣ�$T=\frac{2��m}{Bq}$��
���ӵ��˶�ʱ�䣺t=t1+t2=$\frac{3}{4}$T+$\frac{1}{4}$T=$\frac{2��m}{qB}$��
��3�����ӵ��˶��켣���ų��߽�ֳ�n�ȷݣ�n=2��3��4��������
��ÿ�ȷ�Բ������Բ�Ľ�Ϊ2�ȣ�
�ɼ���֪ʶ�ɵæ�=$\frac{��}{2n}$��tan��=$\frac{r}{R}$��
��ţ�ٵڶ����ɵã�qv0B=m$\frac{{v}_{0}^{2}}{r}$��
��ã�v0=$\frac{qBR}{m}$tan$\frac{��}{2n}$��n=2��3��4��������
��nΪż��ʱ���ɶԳ��Կɵ�t=$\frac{nT}{2}$=$\frac{n��m}{qB}$��n=2��4��6��8����
��nΪ����ʱ��tΪ���ڵ����������ϵ�һ�ε��˶�ʱ�䣬
��t=$\frac{n-1}{2}$T+$\frac{��+\frac{��}{n}}{2��}$T=$\frac{��{n}^{2}+1����m}{nqB}$��n=3��5��7������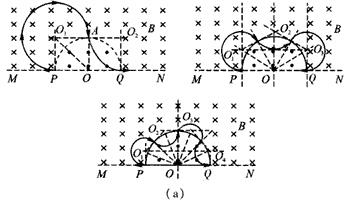
��xΪO�������˶��켣��Բ�ĵľ��룬
�ɼ���֪ʶ�ã�r=Rtan$\frac{��}{2n}$��x=$\frac{R}{cos\frac{��}{2n}}$��
Ҫ�������߽����У�$\frac{R}{cos\frac{��}{2n}}$+Rtan$\frac{��}{2n}$��2R��
��ã�2cos$\frac{��}{2n}$��1+sin$\frac{��}{2n}$��
��n=2ʱ����������ͼ��b����ʾ
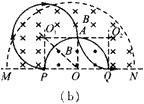
�Ƚϵ�n=3��n=4ʱ���˶��뾶����֪����n=3ʱ���˶��뾶������ӵ��ٶ������
r=Rtan$\frac{��}{2n}$=$\frac{\sqrt{3}}{3}$R=$\frac{m{v}_{0}}{qB}$���ɵã�v0=$\frac{\sqrt{3}qBR}{3m}$�� 
�𣺣�1�����������ڴų�����Բ���˶�������Ϊ$\frac{2��m}{qB}$��
��2����P�㾭���߽�һ�ε�Q�㣬�����˶��ٶȴ�С��$\frac{qBR}{m}$���˶�ʱ����$\frac{2��m}{qB}$��
��3���������Դ�P���ذ뾶���������������������ܵ���Q�㣬���ٶȵ����ֵΪ$\frac{\sqrt{3}qBR}{3m}$��
���� ���⿼���������ڴų��е��˶���Ӧ��ţ�ٵڶ����ɼ�����ȷ���⣬�����������������˶��켣����������ҳ���Ӧ���ٽ���������ȷ�����ǰ����ؼ���

 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�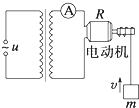 ��ͼ��ʾΪһ�����ѹ����ԭ������Ȧ��������Ϊn��ԭ��Ȧ�ӵ�ѹΪu=U0sin��t�����ҽ����磬����˽���һ��������������һ���綯�����綯������Ȧ����ΪR��������˽�ͨ��Դ�綯������һ����Ϊm������������������ʱ��������ʾ��ΪI���������ٶ�Ϊg������˵����ȷ���ǣ�������
��ͼ��ʾΪһ�����ѹ����ԭ������Ȧ��������Ϊn��ԭ��Ȧ�ӵ�ѹΪu=U0sin��t�����ҽ����磬����˽���һ��������������һ���綯�����綯������Ȧ����ΪR��������˽�ͨ��Դ�綯������һ����Ϊm������������������ʱ��������ʾ��ΪI���������ٶ�Ϊg������˵����ȷ���ǣ�������| A�� | �綯�����˵�ѹΪIR | |
| B�� | ԭ��Ȧ�еĵ���ΪnI | |
| C�� | �綯�����ĵĵ繦��Ϊ$\frac{{U}_{0}I}{n}$ | |
| D�� | ���������������ٶ�Ϊ$\frac{I��{U}_{0}-\sqrt{2}nIR��}{\sqrt{2}nmg}$ |
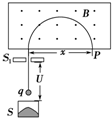 ��������һ�ֲⶨ�������������ͷ���ͬλ�ص���Ҫ���ߣ����Ĺ���ԭ����ͼ������ԴS�����ĸ��ֲ�ͬ�����������ٶȿɿ���Ϊ�㣩�������ٵ糡���ٺ�ֱ�����н���ǿ�ų��������¼���������ƬP�ϣ���������P�ϵ�λ�õ���ڴ�S1�ľ���Ϊx�������ж�
��������һ�ֲⶨ�������������ͷ���ͬλ�ص���Ҫ���ߣ����Ĺ���ԭ����ͼ������ԴS�����ĸ��ֲ�ͬ�����������ٶȿɿ���Ϊ�㣩�������ٵ糡���ٺ�ֱ�����н���ǿ�ų��������¼���������ƬP�ϣ���������P�ϵ�λ�õ���ڴ�S1�ľ���Ϊx�������ж���������
| A�� | ����������ͬλ�أ���xԽС����������Խ�� | |
| B�� | ����������ͬλ�أ���xԽС����������ԽС | |
| C�� | ֻҪx��ͬ������������һ����ͬ | |
| D�� | xԽ�������ӵıȺ�һ��Խ�� |
| A�� | С�������ʱ���������ʱ�� | |
| B�� | С���׳����ʴ���������� | |
| C�� | С���������̼��ٶȵ���������̼��ٶ� | |
| D�� | С����������ƽ������С���������ƽ������ |
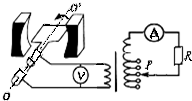 ��ͼ����һ���ΪS������ΪN�ľ���������Ȧ����OO�����ڴŸ�Ӧǿ��ΪB����ǿ�ų����Խ��ٶȦ�����ת������ͼʾλ�ÿ�ʼ��ʱ�������ж���ȷ���ǣ�������
��ͼ����һ���ΪS������ΪN�ľ���������Ȧ����OO�����ڴŸ�Ӧǿ��ΪB����ǿ�ų����Խ��ٶȦ�����ת������ͼʾλ�ÿ�ʼ��ʱ�������ж���ȷ���ǣ�������| A�� | ����������ǵ��������ֵ | |
| B�� | ��ѹ������Ǹ�Ӧ�綯�Ƶ���Чֵ | |
| C�� | ��Ӧ�綯�Ƶ�˲ʱֵ����ʽΪe=NBS��sin��t | |
| D�� | P�����ƶ�ʱ������ʾ����� |
| A�� | ��Ȧ�д�ͨ���仯Խ����Ȧ�в����ĸ�Ӧ�綯��һ��Խ�� | |
| B�� | ��Ȧ�д�ͨ��Խ����Ȧ�в��ĸ�Ӧ�綯��һ��Խ�� | |
| C�� | ��Ȧ���ڴų�Խǿ��λ�ã���Ȧ�в����ĸ�Ӧ�綯��һ��Խ�� | |
| D�� | ��Ȧ�д�ͨ���仯Խ�죬��Ȧ�в����ĸ�Ӧ�綯��Խ�� |
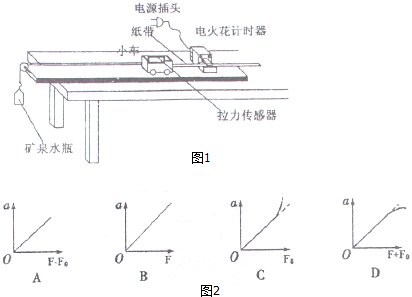
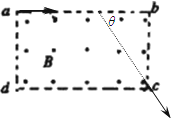 ��ͼ��ʾ������abcd��Χ���д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��ab�ij���ΪL=$\frac{\sqrt{3}mv}{2qB}$�����бȺ�Ϊ$\frac{q}{m}$�������Ӵ�a����ab��������ų����պô�C��ɳ������������ӵ���������
��ͼ��ʾ������abcd��Χ���д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��ab�ij���ΪL=$\frac{\sqrt{3}mv}{2qB}$�����бȺ�Ϊ$\frac{q}{m}$�������Ӵ�a����ab��������ų����պô�C��ɳ������������ӵ���������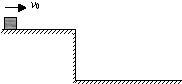 ��ͼ��ʾ����Ϊh=5m��ˮƽƽ̨����һ�����飬���Ҳ��ԵL=5m���Գ��ٶ�v0=6m/s���һ��У���֪������ƽ̨֮��Ķ�Ħ��������=0.2����ȡg=10m/s2��
��ͼ��ʾ����Ϊh=5m��ˮƽƽ̨����һ�����飬���Ҳ��ԵL=5m���Գ��ٶ�v0=6m/s���һ��У���֪������ƽ̨֮��Ķ�Ħ��������=0.2����ȡg=10m/s2��