题目内容
14.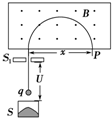 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图,离子源S产生的各种不同正离子束(速度可看作为零),经加速电场加速后垂直进入有界匀强磁场,到达记录它的照相底片P上,设离子在P上的位置到入口处S1的距离为x,可以判断
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造原理如图,离子源S产生的各种不同正离子束(速度可看作为零),经加速电场加速后垂直进入有界匀强磁场,到达记录它的照相底片P上,设离子在P上的位置到入口处S1的距离为x,可以判断( )
| A. | 若离子束是同位素,则x越小,离子质量越大 | |
| B. | 若离子束是同位素,则x越小,离子质量越小 | |
| C. | 只要x相同,则离子质量一定相同 | |
| D. | x越大,则离子的比荷一定越大 |
分析 根据动能定理求出粒子进入磁场的速度,根据牛顿第二定律求出轨道半径,从而得知x与什么因素有关.
解答 解:A、根据动能定理得,qU=$\frac{1}{2}$mv2,得v=$\sqrt{\frac{2qU}{m}}$.
由qvB=m$\frac{{v}^{2}}{r}$ 得,r=$\frac{mv}{qB}$=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$.
则x=2r=$\frac{2}{B}\sqrt{\frac{2mU}{q}}$.
若离子束是同位素,q相同,x越小,对应的离子质量越小.故A错误,B正确.
C、由x=2r=$\frac{2}{B}\sqrt{\frac{2mU}{q}}$知,只要x相同,对应的离子的比荷一定相等,而质量不一定相同.故C错误;
D、由C可知,当x越大,则离子的比荷$\frac{q}{m}$一定越小,故D错误;
故选:B.
点评 解决本题的关键利用动能定理和牛顿第二定律求出P到S1的距离,从而得出x与电荷的比荷有关,及注意电荷的比荷是$\frac{q}{m}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.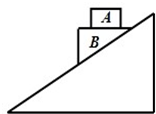 如图,光滑斜面固定于水平地面,滑块B上表面是水平的,滑块A、B保持相对静止,且一起由静止开始下滑,在斜面上运动过程中( )
如图,光滑斜面固定于水平地面,滑块B上表面是水平的,滑块A、B保持相对静止,且一起由静止开始下滑,在斜面上运动过程中( )
 如图,光滑斜面固定于水平地面,滑块B上表面是水平的,滑块A、B保持相对静止,且一起由静止开始下滑,在斜面上运动过程中( )
如图,光滑斜面固定于水平地面,滑块B上表面是水平的,滑块A、B保持相对静止,且一起由静止开始下滑,在斜面上运动过程中( )| A. | A所受的合外力对其不做功 | B. | A只受两个力的作用 | ||
| C. | A对B不做功 | D. | B对A的弹力做正功 |
9.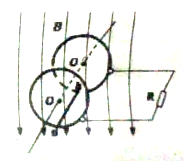 如图所示,在磁感应强度大小为B,方向竖直向下的匀强磁场中,有两个竖直放置,半径为r0的光滑金属圆环通过电刷与阻值为R的电阻串联起来,现将长为L,电阻为r的导体棒ab两个端点分别搭接在两圆环上,并绕与棒ab平行的水平轴OO′(也是两圆环的中心轴)以角速度ω沿圆环做匀速圆周运动,若棒ab始终与两圆环接触良好,圆环电阻不计,则下列说法正确的是( )
如图所示,在磁感应强度大小为B,方向竖直向下的匀强磁场中,有两个竖直放置,半径为r0的光滑金属圆环通过电刷与阻值为R的电阻串联起来,现将长为L,电阻为r的导体棒ab两个端点分别搭接在两圆环上,并绕与棒ab平行的水平轴OO′(也是两圆环的中心轴)以角速度ω沿圆环做匀速圆周运动,若棒ab始终与两圆环接触良好,圆环电阻不计,则下列说法正确的是( )
 如图所示,在磁感应强度大小为B,方向竖直向下的匀强磁场中,有两个竖直放置,半径为r0的光滑金属圆环通过电刷与阻值为R的电阻串联起来,现将长为L,电阻为r的导体棒ab两个端点分别搭接在两圆环上,并绕与棒ab平行的水平轴OO′(也是两圆环的中心轴)以角速度ω沿圆环做匀速圆周运动,若棒ab始终与两圆环接触良好,圆环电阻不计,则下列说法正确的是( )
如图所示,在磁感应强度大小为B,方向竖直向下的匀强磁场中,有两个竖直放置,半径为r0的光滑金属圆环通过电刷与阻值为R的电阻串联起来,现将长为L,电阻为r的导体棒ab两个端点分别搭接在两圆环上,并绕与棒ab平行的水平轴OO′(也是两圆环的中心轴)以角速度ω沿圆环做匀速圆周运动,若棒ab始终与两圆环接触良好,圆环电阻不计,则下列说法正确的是( )| A. | 通过电阻R的电流的大小和方向均不变 | |
| B. | 通过棒ab的感应电流的有效期为$\frac{π{{r}_{0}}^{2}Bω}{\sqrt{2}(R+r)}$ | |
| C. | 电阻R两端的电压的有效值为$\frac{π{{r}_{0}}^{2}BRω}{\sqrt{2}(R+r)}$ | |
| D. | 棒ab在运动过程中收到的最大安培力大小为$\frac{{B}^{2}{L}^{2}ω{r}_{0}}{R+r}$ |
19.关于导体的电阻,下列说法中正确的是( )
| A. | 由R=ρ$\frac{l}{S}$知,导体的电阻与长度l、电阻率ρ成正比,与横截面积S成反比 | |
| B. | 由R=$\frac{U}{l}$可知,导体的电阻跟导体两端的电压成正比,跟导体中的电流成反比 | |
| C. | 将一根导线一分为二,则半根导线的电阻和电阻率都是原来的二分之一 | |
| D. | 金属的电阻率随温度的升高而增大 |
4.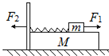 如图所示,一轻弹簧左端固定在长木块M的左端,右端与小物块m连接,且m与M及M与地面间接触面光滑.开始时m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个过程中,对m、M和弹簧组成的系统(整个过程中弹簧形变不超过其弹性限度,M足够长),下面正确的说法是( )
如图所示,一轻弹簧左端固定在长木块M的左端,右端与小物块m连接,且m与M及M与地面间接触面光滑.开始时m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个过程中,对m、M和弹簧组成的系统(整个过程中弹簧形变不超过其弹性限度,M足够长),下面正确的说法是( )
 如图所示,一轻弹簧左端固定在长木块M的左端,右端与小物块m连接,且m与M及M与地面间接触面光滑.开始时m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个过程中,对m、M和弹簧组成的系统(整个过程中弹簧形变不超过其弹性限度,M足够长),下面正确的说法是( )
如图所示,一轻弹簧左端固定在长木块M的左端,右端与小物块m连接,且m与M及M与地面间接触面光滑.开始时m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个过程中,对m、M和弹簧组成的系统(整个过程中弹簧形变不超过其弹性限度,M足够长),下面正确的说法是( )| A. | 由于F1、F2分别对m、M做正功,故系统机械能不断增大 | |
| B. | 当弹簧弹力大小FN与F1、F2大小相等时,m、M的动能最大 | |
| C. | 当弹簧拉伸到最长时,m和M的速度皆为零,系统的机械能最大 | |
| D. | 由于F1、F2等大反向,故系统的机械能守恒 |
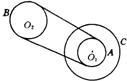 如图所示是一皮带传动装置,O1为两轮的共同轴,由O2带动.已知RB:RA=3:2,RA:RC=1:2,假若皮带不打滑,则分别在三个轮边缘的B、A、C三点角速度之比是3:2:3;线速度之比是1:1:2;向心加速度之比是3:2:6.
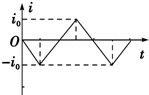
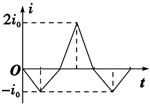
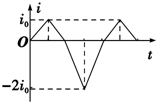
如图所示是一皮带传动装置,O1为两轮的共同轴,由O2带动.已知RB:RA=3:2,RA:RC=1:2,假若皮带不打滑,则分别在三个轮边缘的B、A、C三点角速度之比是3:2:3;线速度之比是1:1:2;向心加速度之比是3:2:6.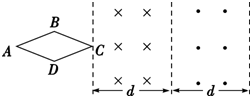 如图所示,三条平行虚线位于纸面内,中间虚线两侧有方向垂直于纸面的匀强磁场,磁感应强度等大反向,菱形闭合导线框ABCD位于纸面内且对角线AC与虚线垂直,磁场宽度与对角线AC长均为d.现使线框沿AC方向匀速穿过磁场,以逆时针方向为感应电流的正方向,则从C点进入磁场到A点离开磁场的过程中,线框中电流i随时间t的变化关系,以下不正确的是( )
如图所示,三条平行虚线位于纸面内,中间虚线两侧有方向垂直于纸面的匀强磁场,磁感应强度等大反向,菱形闭合导线框ABCD位于纸面内且对角线AC与虚线垂直,磁场宽度与对角线AC长均为d.现使线框沿AC方向匀速穿过磁场,以逆时针方向为感应电流的正方向,则从C点进入磁场到A点离开磁场的过程中,线框中电流i随时间t的变化关系,以下不正确的是( )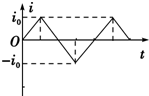
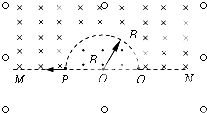 如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求:
如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求: