题目内容
汽车与公路面的动摩擦因数为μ=0.1,公路某转弯处的圆弧半径为R=4 m.
(1)若路面水平,要使汽车转弯时不发生侧滑,汽车速度不能超过多少?(设最大静摩擦力等于滑动摩擦力,取g=10 m/s2)
(2)若将公路转弯处设计成外侧高、内侧低,使路面与水平面有一倾角![]() =5.7°,则当汽车以多大速度转弯时,可使车与路面无摩擦力?
=5.7°,则当汽车以多大速度转弯时,可使车与路面无摩擦力?
解析:
|
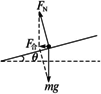
解析:汽车在路面水平转弯时,静摩擦力提供向心力,静摩擦力有最大值,则转弯速度必须受到限制,由此可以运用牛顿第二定律列式求取速度范围.在向内侧倾斜的路面无摩擦转弯时,支持力与重力的合力必须恰好提供向心力,由此切入运用牛顿第二定律列式求取速度即可. (1)汽车在水平路面上转弯不发生侧滑时,沿圆弧运动所需向心力由静摩擦力提供.当车速增大时,静摩擦力也随着增大,当静摩擦力达到最大值μmg时,其对应的车速即为不发生侧滑的最大行驶速度.由牛顿第二定律得μmg=m 求得车速的最大值为 v合max= 可见,若路面水平,要使汽车转弯时不发生侧滑,汽车速度不能超过2 m/s. (2)转弯处路面设计成倾斜的,汽车所受路面的支持力Fn垂直于路面,不再与重力mg在一条直线上,当重力和支持力的合力F合合恰等于汽车转弯所需向心力时,车与路面就无摩擦力,如图所示(将汽车看成质点).由牛顿第二定律得F合合=mgtan v0= 即当汽车以2 m/s速度转弯时,可使车与路面无摩擦力.
方法归纳:注意此处空半格①当在水平路面上转弯时,只有静摩擦力提供向心力,据μmg=m ②当在倾斜路面上转弯,支持力与重力的合力提供向心力时,静摩擦力恰好为零.挖掘静摩擦力为零的隐含条件(Fn与mg的合力恰好提供所需的向心力)是解题的关键.当实际车速v>v0时受到指向内侧的静摩擦力(充当部分向心力),v<v0时,汽车受到指向外侧的静摩擦力. |