题目内容
如图为一条平直公路中的两段,其中A点左边的路段为足够长的柏油路面,A点右边路段为水泥路面.已知汽车轮胎与柏油路面的动摩擦因数为μ1,与水泥路面的动摩擦因数为μ2.当汽车以速度v0在路面行驶时,若刚过A点时紧急刹车后(车轮立即停止转动),汽车要滑行一段距离到B处才能停下;若该汽车以2v0度在柏油路面上行驶,突然发现B处有障碍物,需在A点左侧的柏油路段上某处紧急刹车,若最终汽车刚好撞不上障碍物.(重力加速度为g)

(1)求水泥路面AB段的长度;
(2)在第二种情况下汽车运动了多长时间才停下?

(1)求水泥路面AB段的长度;
(2)在第二种情况下汽车运动了多长时间才停下?
分析:(1)汽车在水泥路上刹车做匀减速直线运动,根据牛顿第二定律求出汽车在水泥路面上的加速度,根据位移速度公式求出水泥路面AB段的长度;
(2)根据题意,汽车如果不撞上障碍物B,则在A点的速度应为v0,根据牛顿第二定律求出在柏油路面上的加速度,根据速度时间公式求出在柏油路上运动的时间及在水泥路面上运动的时间,两段时间之和即为总时间.
(2)根据题意,汽车如果不撞上障碍物B,则在A点的速度应为v0,根据牛顿第二定律求出在柏油路面上的加速度,根据速度时间公式求出在柏油路上运动的时间及在水泥路面上运动的时间,两段时间之和即为总时间.
解答:解:(1)汽车在水泥路面上的加速度为a2,则有:
μ2mg=ma2
又v02=2a2x2
解得:x2=
(2)根据题意,汽车如果不撞上障碍物B,则在A点的速度应为v0,在柏油路面上,μ1mg=ma1,
在柏油路面上运动的时间为t1,则
2v0-v0=a1t1
解得:t1=
水泥路面上,有:μ2mg=ma2
运动时间为t2,则
0-v0=-a2t2
解得:t2=
所以汽车运动的时间t=t1+t2=(
+
)
答:(1)水泥路面AB段的长度为
;
(2)在第二种情况下汽车运动了(
+
)
时间才停下.
μ2mg=ma2
又v02=2a2x2
解得:x2=
| v02 |
| 2gμ2 |
(2)根据题意,汽车如果不撞上障碍物B,则在A点的速度应为v0,在柏油路面上,μ1mg=ma1,
在柏油路面上运动的时间为t1,则
2v0-v0=a1t1
解得:t1=
| v0 |
| μ1g |
水泥路面上,有:μ2mg=ma2
运动时间为t2,则
0-v0=-a2t2
解得:t2=
| v0 |
| μ2g |
所以汽车运动的时间t=t1+t2=(
| 1 |
| μ1 |
| 1 |
| μ2 |
| v0 |
| g |
答:(1)水泥路面AB段的长度为
| v02 |
| 2gμ2 |
(2)在第二种情况下汽车运动了(
| 1 |
| μ1 |
| 1 |
| μ2 |
| v0 |
| g |
点评:本题主要考查了牛顿第二定律及运动学基本公式的直接应用,知道汽车如果不撞上障碍物B,则在A点的速度应为v0,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过
如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过



 如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过
如图所示,在一条平直的公路上有等间距的五个点A、B、C、D、E,相邻两点间距离为L=30m.一辆汽车在公路上做匀加速直线运动,在加速过程中经过这五个点,已知汽车(车头最前端)通过 段和
段和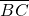 段所用时间分别为3s和2s.试求:
段所用时间分别为3s和2s.试求: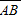 段和
段和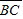 段所用时间分别为3s和2s.试求:
段所用时间分别为3s和2s.试求: