��Ŀ����
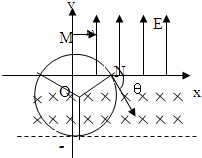
 ��ƽ��ֱ������ϵxOy�У��ڢ���������y�����������ǿ�糡����ǿ��СΪE���ڢڢ�����-d��y��0�ڴ��ڴ�ֱ������ƽ�����ڵ���ǿ�ų���һ����Ϊm�������Ϊ-q�Ĵ���������Ӵ�y���ϵ�M�����ٶȦ�0��ֱ��y������糡����x���ϵ�N����x��������ɦ�=60�������ų���ǡ�ò���Ӵų����±߽�����ų�����ͼ��ʾ���������ӵ���������
��ƽ��ֱ������ϵxOy�У��ڢ���������y�����������ǿ�糡����ǿ��СΪE���ڢڢ�����-d��y��0�ڴ��ڴ�ֱ������ƽ�����ڵ���ǿ�ų���һ����Ϊm�������Ϊ-q�Ĵ���������Ӵ�y���ϵ�M�����ٶȦ�0��ֱ��y������糡����x���ϵ�N����x��������ɦ�=60�������ų���ǡ�ò���Ӵų����±߽�����ų�����ͼ��ʾ���������ӵ�����������1��M��N�����ĵ��Ʋ�U��
��2���ų��ĴŸ�Ӧǿ�ȴ�СB��
��3�����Ӵ�M���˶�����һ���뿪�ų�����ʱ��t��
��������1�������ڵ�һ���ĵ糡������ƽ���˶����ɶ��ܶ����������M��N�����ĵ��Ʋ
��2�������ڴų���������Բ���˶����������ӵ��˶��켣������ѧ֪ʶ������ӵĹ���뾶��
���������ṩ������Բ���˶�������������ţ�ٵڶ����ɿ�������Ÿ�Ӧǿ�ȣ�
��3����������ڴų��е��˶�ʱ�䣬��������ڵ糡������ƽ���˶���ʱ�䣬Ȼ����������ܵ��˶�ʱ�䣮
��2�������ڴų���������Բ���˶����������ӵ��˶��켣������ѧ֪ʶ������ӵĹ���뾶��
���������ṩ������Բ���˶�������������ţ�ٵڶ����ɿ�������Ÿ�Ӧǿ�ȣ�
��3����������ڴų��е��˶�ʱ�䣬��������ڵ糡������ƽ���˶���ʱ�䣬Ȼ����������ܵ��˶�ʱ�䣮
��� �⣺��1�������뿪��һ���ĵ糡ʱ�������ٶ�v=
�⣺��1�������뿪��һ���ĵ糡ʱ�������ٶ�v=
=2v0��
�����ڵ糡������ƽ���˶���
�ɶ��ܶ����ã�qU=
m��2-
m
��
��ã�U=
��
��2�������ڴų���������Բ���˶����˶��켣��ͼ��ʾ��
����ѧ֪ʶ�ɵã�rsin30��+r=d��
��ţ�ٵڶ����ɵã�qBv=m
��
��ã�B=
��
��3�������ڴų�����Բ���˶������ڣ�T=
=
��
�������ڴų��е��˶��켣������ѧ֪ʶ�ɵã�����ת����Բ�Ľ�Ϊ240�㣬
�����ڴų��е��˶�ʱ�䣺t2=
T��
�����뿪�糡ʱ��ֱ����ķ��ٶ�vy=vsin60��=
v0��
��ţ�ٵڶ����ɵã�a=
��
���ȱ����˶����ٶȹ�ʽ��vy=at1��
��ã����ӵ��˶���ʱ�䣺t=t1+t2=
+
��
�𣺣�1��M��N�����ĵ��Ʋ�Ϊ
��
��2���ų��ĴŸ�Ӧǿ�ȴ�СΪ
��
��3�����Ӵ�M���˶�����һ���뿪�ų�����ʱ��Ϊ
+
��
 �⣺��1�������뿪��һ���ĵ糡ʱ�������ٶ�v=
�⣺��1�������뿪��һ���ĵ糡ʱ�������ٶ�v=| v0 |
| cos60�� |
�����ڵ糡������ƽ���˶���
�ɶ��ܶ����ã�qU=
| 1 |
| 2 |
| 1 |
| 2 |
| �� | 2 0 |
��ã�U=
3m
| ||
| 2q |
��2�������ڴų���������Բ���˶����˶��켣��ͼ��ʾ��
����ѧ֪ʶ�ɵã�rsin30��+r=d��
��ţ�ٵڶ����ɵã�qBv=m
| v2 |
| r |
��ã�B=
| 3m��0 |
| qd |
��3�������ڴų�����Բ���˶������ڣ�T=
| 2��r |
| qB |
| 2��m |
| qB |
�������ڴų��е��˶��켣������ѧ֪ʶ�ɵã�����ת����Բ�Ľ�Ϊ240�㣬
�����ڴų��е��˶�ʱ�䣺t2=
| 240 |
| 360 |
�����뿪�糡ʱ��ֱ����ķ��ٶ�vy=vsin60��=
| 3 |
��ţ�ٵڶ����ɵã�a=
| qE |
| m |
���ȱ����˶����ٶȹ�ʽ��vy=at1��
��ã����ӵ��˶���ʱ�䣺t=t1+t2=
| ||
| qE |
| 4��m |
| 3qB |
�𣺣�1��M��N�����ĵ��Ʋ�Ϊ
3m
| ||
| 2q |
��2���ų��ĴŸ�Ӧǿ�ȴ�СΪ
| 3mv0 |
| qd |
��3�����Ӵ�M���˶�����һ���뿪�ų�����ʱ��Ϊ
| ||
| qE |
| 4��m |
| 3qB |
�����������Ǵ��������ڵ糡���ų����˶����ۺ��⣬���������������ӵ��˶��켣��Ӧ����ѧ֪ʶ��������ڴų�����Բ���˶��Ĺ���뾶������ת����Բ�Ľǣ��DZ�����ѵ㣬Ҳ����ȷ����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��2008?�����ƽ��ֱ������ϵxOy�У���I��������y�Ḻ�������ǿ�糡����IV�����ڴ�ֱ������ƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊq�Ĵ���������Ӵ�y���������ϵ�M�����ٶ�v0��ֱ��y������糡����x���ϵ�N����x���������60�������ų�������y�Ḻ�����ϵ�P�㴹ֱ��y������ų�����ͼ��ʾ������������������
��2008?�����ƽ��ֱ������ϵxOy�У���I��������y�Ḻ�������ǿ�糡����IV�����ڴ�ֱ������ƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊq�Ĵ���������Ӵ�y���������ϵ�M�����ٶ�v0��ֱ��y������糡����x���ϵ�N����x���������60�������ų�������y�Ḻ�����ϵ�P�㴹ֱ��y������ų�����ͼ��ʾ������������������ ��ͼ��ʾ����ƽ��ֱ������ϵxOy�У��ڢ���������y�Ḻ����ij�ǿΪE��ǿ�糡���ڢ�����ij�����������ڴ��ڴ�ֱ������ƽ���������ǿ�ų���ͼ��δ���������Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊq�Ĵ���������ӣ�����������������y���ϵ�M����v0�ٶȴ�ֱ��y������糡����x���ϵ�N����x���������30�����������ų������ų�ƫת��ͨ��y���ϵ�P�㣬����P��ʱ���ٶȷ�����y�Ḻ�����60�㣮��
��ͼ��ʾ����ƽ��ֱ������ϵxOy�У��ڢ���������y�Ḻ����ij�ǿΪE��ǿ�糡���ڢ�����ij�����������ڴ��ڴ�ֱ������ƽ���������ǿ�ų���ͼ��δ���������Ÿ�Ӧǿ��ΪB��һ����Ϊm�������Ϊq�Ĵ���������ӣ�����������������y���ϵ�M����v0�ٶȴ�ֱ��y������糡����x���ϵ�N����x���������30�����������ų������ų�ƫת��ͨ��y���ϵ�P�㣬����P��ʱ���ٶȷ�����y�Ḻ�����60�㣮�� ��ͼ��ʾ����ƽ��ֱ������ϵxoy�еĵ�һ�����ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱ������ƽ�����ڵ��н�Բ����ǿ�ų�����ͼ��δ���������ڵڶ������ڴ�����x�Ḻ�������ǿ�糡���糡ǿ�ȴ�СΪE��һ����Դ�̶���x���ϵ�A�㣬A������Ϊ��-L��0��������Դ��y���������ͷų��ٶȴ�СΪv�ĵ��ӣ�����ǡ����ͨ��y���ϵ�C�㣬���Ӿ����ų����ٶ���y�Ḻ������֪���ӵ�����Ϊm�������Ϊe�������ǵ��ӵ������͵���֮�������ã�����
��ͼ��ʾ����ƽ��ֱ������ϵxoy�еĵ�һ�����ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱ������ƽ�����ڵ��н�Բ����ǿ�ų�����ͼ��δ���������ڵڶ������ڴ�����x�Ḻ�������ǿ�糡���糡ǿ�ȴ�СΪE��һ����Դ�̶���x���ϵ�A�㣬A������Ϊ��-L��0��������Դ��y���������ͷų��ٶȴ�СΪv�ĵ��ӣ�����ǡ����ͨ��y���ϵ�C�㣬���Ӿ����ų����ٶ���y�Ḻ������֪���ӵ�����Ϊm�������Ϊe�������ǵ��ӵ������͵���֮�������ã����� ��ѡ���⡿��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��������y�Ḻ�������ǿ�糡�����������ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B=
��ѡ���⡿��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��������y�Ḻ�������ǿ�糡�����������ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B=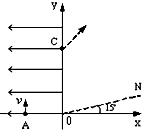 ��ͼ��ʾ����ƽ��ֱ������ϵxoy�еĵ�һ�����ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱ������ƽ�����ڵ��н�Բ����ǿ�ų�����ͼ��δ���������ڵڶ������ڴ�����x�Ḻ�������ǿ�糡��һ����Դ�̶���x���ϵ�A�㣬A������Ϊ��-L��0��������Դ��Y���������ͷų��ٶȴ�СΪv�ĵ��ӣ�����ǡ����ͨ��y���ϵ�C�㣬C������Ϊ��0��2L�������Ӿ����ų���ǡ�ô�ֱͨ����һ��������x���������15��ǵ�����ON����֪���ӵ�����Ϊm�������Ϊe�����������ӵ�����������֮�������ã�����
��ͼ��ʾ����ƽ��ֱ������ϵxoy�еĵ�һ�����ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱ������ƽ�����ڵ��н�Բ����ǿ�ų�����ͼ��δ���������ڵڶ������ڴ�����x�Ḻ�������ǿ�糡��һ����Դ�̶���x���ϵ�A�㣬A������Ϊ��-L��0��������Դ��Y���������ͷų��ٶȴ�СΪv�ĵ��ӣ�����ǡ����ͨ��y���ϵ�C�㣬C������Ϊ��0��2L�������Ӿ����ų���ǡ�ô�ֱͨ����һ��������x���������15��ǵ�����ON����֪���ӵ�����Ϊm�������Ϊe�����������ӵ�����������֮�������ã�����