题目内容
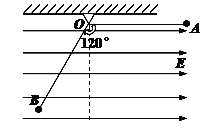
【题目】如图所示，在水平方向的匀强电场中，用长为
不可伸长的绝缘细线拴住一质量为m，带电荷量为+q的小球，线的上端固定于O点。将小球拉到与O点在同一水平面的A处，由静止释放小球，细线转过120o角到达B点时的速度恰好为零，设整个过程中细线始终处于拉直状态，重力加速度为g。求：
（1）匀强电场的场强E的大小；
（2）小球运动过程中的最大速度；
（3）若小球刚运动到最大速度时烧断细线，并从此开始计时，经过3s小球的速度变化量为多少？
【答案】（1）
（2）
（3）
，方向与竖直方向成
角
【解析】（1）从A到B过程由动能定理得：
Eq(L+Lsin30°)-
300=0-0
解得：
=
（2）当电场力与重力的合力与细绳在同一条直线上时，小球的速度最大，设为v，此时细绳与竖直方向的夹角为300 ，从A到速度最大位置过程中，由动能定理得：
-Eq(L-Lsin300)+mgLcos300=
mv2-0
解得v=
（3）细绳被烧断后，小球所受电场力与重力的合力与速度垂直，小球做类平抛运动
由mg/cos300=ma
得a=
根据Δv=at
可得小球3s内的速度变化量为2
g，方向与竖直方向成300角向下
练习册系列答案
相关题目
