题目内容
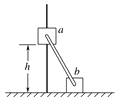
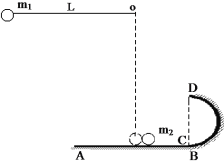
【题目】如图所示,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动。一长L为0.8 m的细绳,一端固定于O点,另一端系一个质量![]() 为0.2 kg的小球。当小球在竖直方向静止时,球对水平桌面的作用力刚好为零。现将球提起使细绳处于水平位置时无初速释放。当小球
为0.2 kg的小球。当小球在竖直方向静止时,球对水平桌面的作用力刚好为零。现将球提起使细绳处于水平位置时无初速释放。当小球![]() 摆至最低点时,细绳恰好被拉断,此时小球
摆至最低点时,细绳恰好被拉断,此时小球![]() 恰好与放在桌面上的质量
恰好与放在桌面上的质量![]() 为0.8kg的小球正碰,碰后
为0.8kg的小球正碰,碰后![]() 以2 m/s的速度弹回,
以2 m/s的速度弹回,![]() 将沿半圆形轨道运动。两小球均可视为质点,取g=10m/s2。求:
将沿半圆形轨道运动。两小球均可视为质点,取g=10m/s2。求:
(1)细绳所能承受的最大拉力为多大?
(2)![]() 在半圆形轨道最低点C点的速度为多大?
在半圆形轨道最低点C点的速度为多大?
(3)为了保证![]() 在半圆形轨道中运动时不脱离轨道,试讨论半圆形轨道的半径R应该满足的条件。
在半圆形轨道中运动时不脱离轨道,试讨论半圆形轨道的半径R应该满足的条件。
【答案】(1)6N(2)1.5 m/s(3)R≤0.045 m或R≥0.1125m
【解析】
试题分析:(1)设小球![]() 摆至最低点时速度为v0,由机械能守恒定律,得:
摆至最低点时速度为v0,由机械能守恒定律,得:
![]()
解得:![]()
小球![]() 在最低点时,由牛顿第二定律,得:
在最低点时,由牛顿第二定律,得:![]()
解得:![]() =6N
=6N
(2)![]() 与
与![]() 碰撞,动量守恒,设
碰撞,动量守恒,设![]() 、
、![]() 碰后的速度分别为v1、v2,选向右的方向为正方向,则
碰后的速度分别为v1、v2,选向右的方向为正方向,则![]()
解得:v2=1.5 m/s
(3) ①若小球![]() 恰好通过最高点D点,由牛顿第二定律,得:
恰好通过最高点D点,由牛顿第二定律,得:
![]()
![]() 在CD轨道上运动时,由机械能守恒定律,得:
在CD轨道上运动时,由机械能守恒定律,得: ![]()
解得:R1=0.045 m.
②若小球恰好到达圆轨道与圆心等高处速度减为0,则有:
![]()
解得:R2=0.1125m
综上:R应该满足R≤0.045 m或R≥0.1125m

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目