题目内容
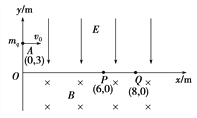
【题目】如图所示,在直角坐标系xOy的第一象限中分布着沿y轴负方向的匀强电场,在第四象限中分布着垂直纸面向里的匀强磁场.一个质量为m、电荷量为+q的微粒,在点A(0,3)以初速度v0=120 m/s平行x轴正方向射入电场区域,然后从电场区域进入磁场,又从磁场进入电场,并且先后只通过x轴上的P点(6,0)和Q点(8,0)各一次.已知该微粒的比荷为![]() =1×102 C/kg,微粒重力不计,求:
=1×102 C/kg,微粒重力不计,求:
(1)微粒从A到P所经历的时间和加速度的大小;
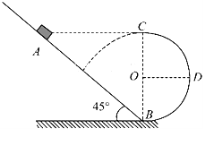
(2)求出微粒到达P点时速度方向与x轴正方向的夹角,并画出带电微粒在电场和磁场中由A至Q的运动轨迹;
(3)电场强度E和磁感应强度B的大小.
【答案】(1)0.05 s 2.4×103 m/s2 (2)45° 如图;

(3)24 N/C 1.2 T
【解析】(1)微粒从平行x轴正方向射入电场区域,由A到P做类平抛运动,微粒在x轴正方向做匀速直线运动,
由x=v0t,得t=![]() =0.05 s,
=0.05 s,
微粒沿y轴负方向做初速度为零的匀加速直线运动,由y=![]() at2,
at2,
得a=2.4×103 m/s2.
(2)vy=at,tan α=![]() =1,所以α=45°.
=1,所以α=45°.
轨迹如图:

(3)由qE=ma,得E=24 N/C
设微粒从P点进入磁场以速度v做匀速圆周运动,v=![]() v0=120
v0=120![]() m/s,
m/s,
由![]() ,得
,得![]() ,
,
由几何关系,可知r=![]() m,可得B=
m,可得B=![]() =1.2 T.
=1.2 T.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目