题目内容
【题目】（17分）如图所示，倾角为45°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相接，O为轨道圆心，BC为圆轨道直径且处于竖直平面内，A、C两点等高。质量m=1kg的滑块（可视为质点）从A点由静止开始下滑，恰能滑到与O等高的D点，g取10m/s2。
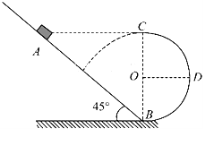
（1）若使滑块能到达C点，求滑块至少从离地多高处由静止开始下滑；
（2）若滑块离开C处后恰能垂直打在斜面上，求滑块经过C点时对轨道的压力；
（3)若使滑块在圆弧在BDC段不脱离轨道，则A下滑的高度应该满足什么条件。
【答案】（1）2m（2）3.3N（3）A下滑的高度h≥2m或h≤0.8m
【解析】
试题分析：(1)由A到D，根据动能定理可得 mg（2R-R)-μmgcos45°
=0 （1分）
解得 
（1分）
若滑块恰能到达C点，
（1分）
得
=2m/s （1分）
从高为H的最高点到C的过程，
根据动能定理 mg(H-2R)-μmgcos45°
=
（1分）
解得H=2m （1分）
（2）离开C点后滑块做平抛运动，垂直打到斜面上时有
（1分）
（1分）
（1分）
（1分）
解得
（1分）
在C点，根据牛顿第二定律有
（1分）
求得：
（1分）
由牛顿第三定律可知，滑块对轨道的压力为
（1分）
方向竖直向上 （1分）
（3）由题意可知，滑块从A处，即距地面高度为2R=0.8m处下滑恰好到达D点，所以，若使滑块在圆弧在BDC段不脱离轨道，则A下滑的高度h≥2m或h≤0.8m。（2分）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
