题目内容
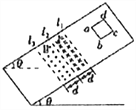
【题目】如图所示为一上、下表面面积足够大的玻璃砖，玻璃砖内有一圆锥真空区，圆锥顶角∠ACB= 90°，圆锥底面与玻璃砖上、下表面平行，圆锥底面AB的中点O处有一红色点光源，光线只射向AB上方区域。O点离玻璃砖上表面距离5d，圆锥顶点C离玻璃砖上表面的距离为dtan75°。已知玻璃对红光的折射率n= 
，求玻璃砖上表面有光线射出的区域的面积。（不考虑光线的反射）
【答案】
【解析】光线由玻璃射向真空，临界角满足
解得C=450
如图，光源O发出的临界光线1的光路如图，由折射率公式： 
解得θ=300
由几何关系，光线到达玻璃砖上表面的入射角为α=150
又α<C，所以光线1能够射出水面；由几何关系r1=d
如图所示，光源O发出的临界光线2的光路如图，且光线2恰好在玻璃砖上表面发生全反射，由几何关系r2=5d
综上，光线射出玻璃砖上表面的形状是环形，其面积为
练习册系列答案
相关题目
