Question

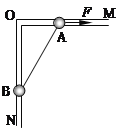
【题目】如图所示，竖直平面内放一直角杆MON，OM水平，ON竖直且光滑，用不可伸长的轻绳相连的两小球A和B分别套在OM和ON杆上，B球的质量为2 kg，在作用于A球的水平力F的作用下，A、B均处于静止状态，此时OA="0.3" m，OB="0.4" m，改变水平力F的大小，使A球向右加速运动，已知A球向右运动0.1m时速度大小为3m/s，则在此过程中绳对B球的拉力所做的功为(取g="10" m/s2)

A. 11 JB. 16 JC. 18 JD. 9 J

Answer 1

【答案】C

【解析】

试题A球向右运动0．1m时，由几何关系得，B上升距离：h=0．4m-m=0．1m；此时细绳与水平方向夹角的正切值：tanθ=，则得 cosθ=，sinθ=由运动的合成与分解知识可知：B球的速度为 vBsinθ=vAcosθ，可得 vB=4m/s；以B球为研究对象，由动能定理得：WF-mgh=mvB2,代入数据解得：WF="18J," 即绳对B球的拉力所做的功为18J；故选C．