题目内容
 如图所示,在铅板A上有一个发射源C,可向各个方向射出速率v0=2.8×106m/s的电子,B为金属网,A、B连接在电路上,电源电动势E=20V,内阻不计,滑动变阻器范围为0~20Ω,A、B间距d=10cm,M为荧光屏(足够大),它紧挨着金属网外侧,已知电子的比荷
如图所示,在铅板A上有一个发射源C,可向各个方向射出速率v0=2.8×106m/s的电子,B为金属网,A、B连接在电路上,电源电动势E=20V,内阻不计,滑动变阻器范围为0~20Ω,A、B间距d=10cm,M为荧光屏(足够大),它紧挨着金属网外侧,已知电子的比荷| e | m |
(1)A、B间场强大小;
(2)不同方向射出的电子到达荧光屏的时间不同,则电子到达荧光屏的最长时间和电子到达荧光屏范围的最大宽度是多少;
(3)调节R使粒子打在荧光屏上面积范围缩小为原来一半,此时调节Rap多大?
分析:(1)先根据欧姆定律计算AB间的电压,再根据E=
,即可求解;
(2)平行板射出的电子,当初速度平行极板射出时,运动时间最长,此时电子在电场力作用下做类平抛运动,平行极板方向做匀速直线运动,垂直极板方向做匀加速直线运动,根据平抛运动的规律即可解题;
(3)荧光屏范围是个圆形,根据圆形面积公式算出面积的表达式,进而求出此时调节Rap的电阻.
| U |
| d |
(2)平行板射出的电子,当初速度平行极板射出时,运动时间最长,此时电子在电场力作用下做类平抛运动,平行极板方向做匀速直线运动,垂直极板方向做匀加速直线运动,根据平抛运动的规律即可解题;
(3)荧光屏范围是个圆形,根据圆形面积公式算出面积的表达式,进而求出此时调节Rap的电阻.
解答:解:(1)设滑动变阻器最大阻值为R0,
有U=
E
A、B间场强E′=
=
E=56V/m
(2)平行板射出的电子,当初速度平行极板射出时,运动时间最长,此时电子在电场力作用下做类平抛运动,平行极板方向做匀速直线运动,垂直极板方向做匀加速直线运动,则有:
d=
atm2=
tm2
解得:tm=
×10-6s≈1.43×10-7s
平行极板方向做匀速直线运动,
所以荧光屏范围的最大宽度:dm=2v0tm=0.8m
(3)荧光屏范围面积为:
S=πr2=π(v0tm)2=
?
所以S正比于
因为S′=
S,有R′ap=2Rap=11.2Ω
答:(1)A、B间场强大小为56V/m;
(2)不同方向射出的电子到达荧光屏的时间不同,则电子到达荧光屏的最长时间和电子到达荧光屏范围的最大宽度是0.8m;
(3)调节R使粒子打在荧光屏上面积范围缩小为原来一半,此时调节Rap为11.2Ω;
有U=
| Rap |
| R0 |
A、B间场强E′=
| U |
| d |
| Rap |
| R0d |
(2)平行板射出的电子,当初速度平行极板射出时,运动时间最长,此时电子在电场力作用下做类平抛运动,平行极板方向做匀速直线运动,垂直极板方向做匀加速直线运动,则有:
d=
| 1 |
| 2 |
| 1 |
| 2 |
| E′e |
| m |
解得:tm=
| 1 |
| 7 |
平行极板方向做匀速直线运动,
所以荧光屏范围的最大宽度:dm=2v0tm=0.8m
(3)荧光屏范围面积为:
S=πr2=π(v0tm)2=
| 2mπv0R0d2 |
| eE |
| 1 |
| Rap |
所以S正比于
| 1 |
| Rap |
因为S′=
| 1 |
| 2 |
答:(1)A、B间场强大小为56V/m;
(2)不同方向射出的电子到达荧光屏的时间不同,则电子到达荧光屏的最长时间和电子到达荧光屏范围的最大宽度是0.8m;
(3)调节R使粒子打在荧光屏上面积范围缩小为原来一半,此时调节Rap为11.2Ω;
点评:当极板之间的电压最大时,亮斑的半径最小,并且运动的最远的电子应该是平行于A板发出的,即此时的电子在电场中做的是类平抛运动.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2011?湖北模拟)如图所示,在铅板A上放一个放射源C,可向各个方向射出速率为v的β射线,B为金属网,A、B连接在电路上,电源电动势为E,内阻为r,滑动变阻器的总阻值为R.图中滑动变阻器滑片置于中点,AB间的间距为d,M为足够大的荧光屏,M紧挨着金属网外侧.已知β粒子质量为m,电量为e.不计β射线所形成的电流对电路的影响,求:
(2011?湖北模拟)如图所示,在铅板A上放一个放射源C,可向各个方向射出速率为v的β射线,B为金属网,A、B连接在电路上,电源电动势为E,内阻为r,滑动变阻器的总阻值为R.图中滑动变阻器滑片置于中点,AB间的间距为d,M为足够大的荧光屏,M紧挨着金属网外侧.已知β粒子质量为m,电量为e.不计β射线所形成的电流对电路的影响,求: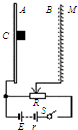 如图所示,在铅板A上有一个放射源C可向各个方向射出速率v为2.04×107 m/s的β射线,B为金属网,A、B连接在电路上,电源电动势E为15V,内阻r为2.5Ω,滑动变阻器在0~10Ω之间可调.图中滑动变阻器滑片置于中点,A、B间距d为10cm,M为荧光屏(足够大),它紧挨着金属网外侧,β粒子穿过金属网打到荧光屏时,荧光屏上就会出现亮斑.已知β粒子的比荷e/m为1.7×1011 C/kg,不计β射线所形成的电流对电路的影响.求:
如图所示,在铅板A上有一个放射源C可向各个方向射出速率v为2.04×107 m/s的β射线,B为金属网,A、B连接在电路上,电源电动势E为15V,内阻r为2.5Ω,滑动变阻器在0~10Ω之间可调.图中滑动变阻器滑片置于中点,A、B间距d为10cm,M为荧光屏(足够大),它紧挨着金属网外侧,β粒子穿过金属网打到荧光屏时,荧光屏上就会出现亮斑.已知β粒子的比荷e/m为1.7×1011 C/kg,不计β射线所形成的电流对电路的影响.求: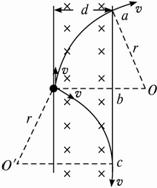
 的
的 射线,B为金属网,A、B连接在电路上,电源电动势为
射线,B为金属网,A、B连接在电路上,电源电动势为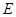 ,内阻为
,内阻为 ,滑动变阻器总阻值为
,滑动变阻器总阻值为 ,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知
,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知 ,不计
,不计