题目内容
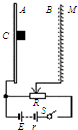 如图所示,在铅板A上有一个放射源C可向各个方向射出速率v为2.04×107 m/s的β射线,B为金属网,A、B连接在电路上,电源电动势E为15V,内阻r为2.5Ω,滑动变阻器在0~10Ω之间可调.图中滑动变阻器滑片置于中点,A、B间距d为10cm,M为荧光屏(足够大),它紧挨着金属网外侧,β粒子穿过金属网打到荧光屏时,荧光屏上就会出现亮斑.已知β粒子的比荷e/m为1.7×1011 C/kg,不计β射线所形成的电流对电路的影响.求:
如图所示,在铅板A上有一个放射源C可向各个方向射出速率v为2.04×107 m/s的β射线,B为金属网,A、B连接在电路上,电源电动势E为15V,内阻r为2.5Ω,滑动变阻器在0~10Ω之间可调.图中滑动变阻器滑片置于中点,A、B间距d为10cm,M为荧光屏(足够大),它紧挨着金属网外侧,β粒子穿过金属网打到荧光屏时,荧光屏上就会出现亮斑.已知β粒子的比荷e/m为1.7×1011 C/kg,不计β射线所形成的电流对电路的影响.求:(1)闭合电键S后,AB间的场强的大小;
(2)β粒子到达金属网B的最长时间;
(3)切断电键S,并撤去金属网B,加上垂直纸面向内,范围足够大的匀强磁场,磁感应强度大小B=6.0×10-4 T,这时在竖直方向上能观察到荧光屏亮斑的长度.
分析:(1)由闭合电路欧姆定律求出电容器板间的电压UAB,由E=
求出AB间的场强大小.
(2)β粒子在两板间运动只受电场力作用,其加速度是一定的,沿A板方向射出的β粒子运动到达B板所用的时间最长,由牛顿第二定律和运动学公式结合求出β粒子到达金属网B的最长时间;
(3)β粒子垂直进入磁场只受洛伦兹力作用做匀速圆周运动,画出轨迹,由牛顿第二定律求出其轨迹,根据几何知识求解在竖直方向上能观察到荧光屏亮斑的长度.
| UAB |
| d |
(2)β粒子在两板间运动只受电场力作用,其加速度是一定的,沿A板方向射出的β粒子运动到达B板所用的时间最长,由牛顿第二定律和运动学公式结合求出β粒子到达金属网B的最长时间;
(3)β粒子垂直进入磁场只受洛伦兹力作用做匀速圆周运动,画出轨迹,由牛顿第二定律求出其轨迹,根据几何知识求解在竖直方向上能观察到荧光屏亮斑的长度.
解答: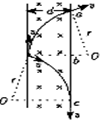 解:(1)由闭合电路欧姆定律得:I=
解:(1)由闭合电路欧姆定律得:I=
=
A=1.2 A?
UAB=
IR=1.2×10/2V=6.0V?
由EAB=
=
V/m=60V/m
(2)β粒子在两板间运动只受电场力作用,其加速度为?
a=
=1.02×1013m/s2
分析可知,沿A板方向射出的β粒子运动到达B板所用的时间最长?
根据:d=
a?t2?
∴t=
=
≈1.4×10-7s?
(3)β粒子垂直进入磁场只受洛伦兹力作用做匀速圆周运动?
有:evB=m
?
得:r=
?
代入解得:r=0.2 m
如图所示,荧光屏亮斑区的上边界就是沿A板射出的β粒子所达到的a点,有:
(r-d)2+
2=r2
?
=
=
=0.17 m?
荧光屏亮斑区的下边界就是β粒子轨迹与屏相切的c点
有:(r-d)2+
2=r2?
得:
=0.17 m
在竖直方向上亮斑区的长度为:
=0.17 m+0.17 m=0.34 m
答:
(1)闭合电键S后,AB间的场强的大小是60V/m;
(2)β粒子到达金属网B的最长时间是1.4×10-7s;
(3)在竖直方向上亮斑区的长度为0.34m.
 解:(1)由闭合电路欧姆定律得:I=
解:(1)由闭合电路欧姆定律得:I=| E |
| R+r |
| 15 |
| 10+2.5 |
UAB=
| 1 |
| 2 |
由EAB=
| UAB |
| d |
| 6 |
| 0.1 |
(2)β粒子在两板间运动只受电场力作用,其加速度为?
a=
| eE |
| m |
分析可知,沿A板方向射出的β粒子运动到达B板所用的时间最长?
根据:d=
| 1 |
| 2 |
∴t=
|
|
(3)β粒子垂直进入磁场只受洛伦兹力作用做匀速圆周运动?
有:evB=m
| v2 |
| r |
得:r=
| mv |
| eB |
代入解得:r=0.2 m
如图所示,荧光屏亮斑区的上边界就是沿A板射出的β粒子所达到的a点,有:
(r-d)2+
. |
| ab |
?
. |
| ab |
| d(2r-d) |
| 0.1×(2×0.2-0.1) |
荧光屏亮斑区的下边界就是β粒子轨迹与屏相切的c点
有:(r-d)2+
. |
| bc |
得:
. |
| bc |
在竖直方向上亮斑区的长度为:
. |
| ac |
答:
(1)闭合电键S后,AB间的场强的大小是60V/m;
(2)β粒子到达金属网B的最长时间是1.4×10-7s;
(3)在竖直方向上亮斑区的长度为0.34m.
点评:本题是磁场、电路、电场和力学等知识的综合应用,画出轨迹是电子磁场中运动时研究的基本方法.

练习册系列答案
相关题目
 (2011?湖北模拟)如图所示,在铅板A上放一个放射源C,可向各个方向射出速率为v的β射线,B为金属网,A、B连接在电路上,电源电动势为E,内阻为r,滑动变阻器的总阻值为R.图中滑动变阻器滑片置于中点,AB间的间距为d,M为足够大的荧光屏,M紧挨着金属网外侧.已知β粒子质量为m,电量为e.不计β射线所形成的电流对电路的影响,求:
(2011?湖北模拟)如图所示,在铅板A上放一个放射源C,可向各个方向射出速率为v的β射线,B为金属网,A、B连接在电路上,电源电动势为E,内阻为r,滑动变阻器的总阻值为R.图中滑动变阻器滑片置于中点,AB间的间距为d,M为足够大的荧光屏,M紧挨着金属网外侧.已知β粒子质量为m,电量为e.不计β射线所形成的电流对电路的影响,求: 如图所示,在铅板A上有一个发射源C,可向各个方向射出速率v0=2.8×106m/s的电子,B为金属网,A、B连接在电路上,电源电动势E=20V,内阻不计,滑动变阻器范围为0~20Ω,A、B间距d=10cm,M为荧光屏(足够大),它紧挨着金属网外侧,已知电子的比荷
如图所示,在铅板A上有一个发射源C,可向各个方向射出速率v0=2.8×106m/s的电子,B为金属网,A、B连接在电路上,电源电动势E=20V,内阻不计,滑动变阻器范围为0~20Ω,A、B间距d=10cm,M为荧光屏(足够大),它紧挨着金属网外侧,已知电子的比荷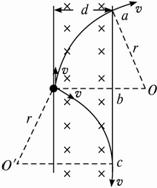
 的
的 射线,B为金属网,A、B连接在电路上,电源电动势为
射线,B为金属网,A、B连接在电路上,电源电动势为 ,内阻为
,内阻为 ,滑动变阻器总阻值为
,滑动变阻器总阻值为 ,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知
,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知 ,不计
,不计