题目内容
 如图所示,质量m=4kg的小物块在与水平方向成θ=37°角的恒力F作用下,从静止开始向右做匀加速运动,已知小物块与水平地面间的动摩擦因数为μ=0.5.经过tl=2s后撤去恒力F,小物块继续向前运动t2=4s后停下.重力加速度g取10m/s2.(sin53°=0.8,cos53°=0.6)求:
如图所示,质量m=4kg的小物块在与水平方向成θ=37°角的恒力F作用下,从静止开始向右做匀加速运动,已知小物块与水平地面间的动摩擦因数为μ=0.5.经过tl=2s后撤去恒力F,小物块继续向前运动t2=4s后停下.重力加速度g取10m/s2.(sin53°=0.8,cos53°=0.6)求:(1)恒力F的大小;
(2)小物块的总位移x.
分析:(1)物体先做匀加速直线运动,后匀减速直线运动,根据牛顿牛顿第二定律分别求出两个过程与F的关系式,根据速度公式得到t1秒末物体的速度为v与tl和tl的关系式,联立求F.
(2)根据位移公式分别求出两段位移,再求解总位移.
(2)根据位移公式分别求出两段位移,再求解总位移.
解答:解:(1)设力F撤去之前物体的加速度为a1,t1秒末物体的速度为v,
根据牛顿第二定律可得:
Fcosθ-μ(mg-Fsinθ)=ma1
由运动学公式得:v=a1t1
设力F撤去之后物体的加速度大小为a2,根据牛顿第二定律可得:μmg=ma2
由运动学公式得:
v=a2t2
联立以上各式得:F=54.5N
(2)设t1秒内物体的位移为x1,t2秒内物体的位移为x2,
由上解得:a1=10m/s2,a2=5m/s2.
x1=
a1t12=
×10×22m=20m
x2=
a2t22=
×5×42m=40m
所以物体的总位移x=x1+x2=60m
答:
(1)恒力F的大小F=54.5N;
(2)小物块的总位移x=60m.
根据牛顿第二定律可得:
Fcosθ-μ(mg-Fsinθ)=ma1
由运动学公式得:v=a1t1
设力F撤去之后物体的加速度大小为a2,根据牛顿第二定律可得:μmg=ma2
由运动学公式得:
v=a2t2
联立以上各式得:F=54.5N
(2)设t1秒内物体的位移为x1,t2秒内物体的位移为x2,
由上解得:a1=10m/s2,a2=5m/s2.
x1=
| 1 |
| 2 |
| 1 |
| 2 |
x2=
| 1 |
| 2 |
| 1 |
| 2 |
所以物体的总位移x=x1+x2=60m
答:
(1)恒力F的大小F=54.5N;
(2)小物块的总位移x=60m.
点评:本题属于知道运动情况求解受力情况的类型,对于第1问,也可以根据动量定理这样列式:[Fcosθ-μ(mg-Fsinθ)]t1-μmgt2=0,求得F=54.5N.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求:
如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求: 如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求:
如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求: (2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求:
(2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求: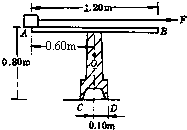 质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?
质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少? 如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.
如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.