题目内容
 如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.
如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.分析:第一秒过程木块和木板都加速,先根据牛顿第二定律求解加速度,然后根据运动学公式确定1s末的速度和位移;撤去推力后,再次求解两个物体的加速度,求解得到速度相同时刻的位移和速度;在B与墙壁碰撞后,先根据动量守恒定律求解共同速度,再根据动能定理求解相对位移;最后再根据功能关系列式求解内能的增加量.
解答:解:以A为研究对象,由牛顿第二定律有:a1=μg=2 m/s2
以B为研究对象,由牛顿第二定律有:a2=
=4m/s2
设撤去推力时A向右速度为v1,对地位移为s1,相对于B向左滑动△s1,则有:
v1=a1t=2m/s s1=
a1t2=1m
设撤去推力时B向右速度为v2,B对地位移为s2,则:
v2=
a2t=4m/s
s2=a2t2=2 m
△s1=s2-s1=1 m
撒去F后,A向右加速,B向右减速;
设B前进s3,尚未与墙壁相碰,两者达到共同速度v3,此时A相对B又向左滑动△s2,由系统动量守恒定律:
mv1+Mv2=(m+M)v3
以B为研究对象,由动能定理:
-μmgs3=
M
-
M
由系统功能关系:
μmg△s2=
M
+
M
-
(m+M)
解得:
s3=3.04 m
△s2=0.8 m
因s2+s3<s,故当两者达到共同速度时,B尚未与墙壁碰撞.B与墙壁发生弹性碰撞后,设A、B再次达到共同速度v4时,A尚未滑离B,A相对于B向右滑动△s3,由系统动量守恒定律:
Mv3-mv3=(M+m)v4
由系统功能关系:
μmg△s3=
(M+m)
-
(M+m)
由上面两式求得△s3=10.4 m
因△s3>△s1+△s2+
=3.8 m,故在两者达到共同速度前,A已经从B右端滑出,故A在B上滑动的整个过程中,A、B系统因摩擦产生内能增量为:
△E=μmg[2(△s1+△s2)+
]=11.2J
答:A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量为11.2J.
以B为研究对象,由牛顿第二定律有:a2=
| F-μmg |
| M |
设撤去推力时A向右速度为v1,对地位移为s1,相对于B向左滑动△s1,则有:
v1=a1t=2m/s s1=
| 1 |
| 2 |
设撤去推力时B向右速度为v2,B对地位移为s2,则:
v2=
| 1 |
| 2 |
s2=a2t2=2 m
△s1=s2-s1=1 m
撒去F后,A向右加速,B向右减速;
设B前进s3,尚未与墙壁相碰,两者达到共同速度v3,此时A相对B又向左滑动△s2,由系统动量守恒定律:
mv1+Mv2=(m+M)v3
以B为研究对象,由动能定理:
-μmgs3=
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| v | 2 2 |
由系统功能关系:
μmg△s2=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
解得:
s3=3.04 m
△s2=0.8 m
因s2+s3<s,故当两者达到共同速度时,B尚未与墙壁碰撞.B与墙壁发生弹性碰撞后,设A、B再次达到共同速度v4时,A尚未滑离B,A相对于B向右滑动△s3,由系统动量守恒定律:
Mv3-mv3=(M+m)v4
由系统功能关系:
μmg△s3=
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| v | 2 4 |
由上面两式求得△s3=10.4 m
因△s3>△s1+△s2+
| L |
| 2 |
△E=μmg[2(△s1+△s2)+
| L |
| 2 |
答:A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量为11.2J.
点评:本题是一道高三后期的压轴题,关键理清两个物体的运动规律,中间分过程多次运用牛顿第二定律、运动学公式、功能关系、动量守恒定律列式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求:
如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求: 如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求:
如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求: (2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求:
(2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求: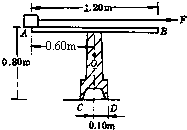 质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?
质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?