题目内容
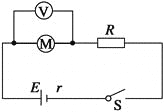
【题目】如图所示的电路中,所用电源的电动势E=6 V,内电阻r=2 Ω,电阻R1可调。现将R1调到4Ω后固定。已知R2=6 Ω,R3=12 Ω,求:
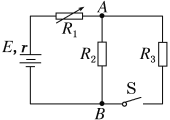
(1)开关S断开和接通时,通过R1的电流分别为多大?
(2)为了使A、B之间电路的电功率在开关S接通时能达到最大值,应将R1的阻值调到多大?这时A、B间消耗的最大电功率是多少?
【答案】(1)0.5A;0.6A (2)当R1=0时,总电流最大,A、B之间的电功率才最大。PAB=4W
【解析】
(1)根据闭合电路的欧姆定律求解开关S断开和接通时,通过R1的电流;(2)开关接通时,A、B之间的总电阻R23=4Ω为定值,所以,只有当R1′=0时,总电流最大,A、B之间的电功率才最大。
(1)开关S断开时,I1=![]() =0.5 A
=0.5 A
开关接通时,R2、R3并联的总电阻R23=![]() =4Ω
=4Ω
I1′=![]() =0.6A
=0.6A
(2)开关接通时,A、B之间的总电阻R23=4Ω为定值,所以,只有当R1′=0时,总电流最大,A、B之间的电功率才最大。
I=![]() =1A
=1A
PAB=I2R23=4W

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目