Question

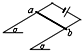
.如图所示，质量为m的跨接杆ab可以无摩擦地沿水平的导轨滑行，两轨间距为L，导轨一端与电阻R连接，放在竖直向下的匀强磁场中，磁感应强度为B。杆从x轴原点O以大小为v₀的水平初速度向右滑行，直到停下。已知杆在整个运动过程中速度v和位移x的函数关系是：v＝v₀－。杆与导轨的电阻不计。

（1）试求杆所受的安培力F随其位移x变化的函数式；
（2）分别求出杆开始运动和停止运动时所受的安培力F₁和F₂；
（3）证明杆在整个运动过程中动能的增量DE_k等于安培力所做的功W；
（4）求出电阻R所增加的内能DE。

Answer 1

(1) F＝＝－ (2) v’＝0，F’＝0
（3）W＝＝mv₀²＝DE_k，
（4）DE＝DE_k＝mv₀²

（1）安培力F＝BIL，I＝，由题意得v＝v₀－，所以F＝＝－，成线性关系。
（2）开始运动瞬间x＝0，F₀＝，停止运动时v’＝0，F’＝0，
（3）安培力与位移成线性关系，所以安培力做的功与平均力做的功相等，即W＝x_m＝x_m，由v’＝v₀－＝0，得x_m＝，所以W＝＝mv₀²＝DE_k，命题得证，
（4）根据能量守恒DE＝DE_k＝mv₀²