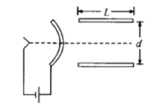
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΨχ‘Β¥÷≤ΎΒΡΥ°ΤΫΟφ…œœύΨύΈΣ![]()
![]() ΒΡ
ΒΡ![]() ΓΔ
ΓΔ![]() ΝΫ¥ΠΖ÷±πΙΧΕ®ΒγΝΩ≤ΜΒ»ΒΡ’ΐΒγΚ…Θ§ΝΫΒγΚ…ΒΡΈΜ÷ΟΉχ±ξ»γΆΦΘ®ΦΉΘ©Υυ ΨΘ§“―÷Σ
ΝΫ¥ΠΖ÷±πΙΧΕ®ΒγΝΩ≤ΜΒ»ΒΡ’ΐΒγΚ…Θ§ΝΫΒγΚ…ΒΡΈΜ÷ΟΉχ±ξ»γΆΦΘ®ΦΉΘ©Υυ ΨΘ§“―÷Σ![]() ¥ΠΒγΚ…ΒΡΒγΝΩΈΣ+
¥ΠΒγΚ…ΒΡΒγΝΩΈΣ+![]() Θ°ΆΦΘ®““Θ© «
Θ°ΆΦΘ®““Θ© «![]() Ν§œΏ÷°ΦδΒΡΒγ ΤΠ’”κΈΜ÷Ο
Ν§œΏ÷°ΦδΒΡΒγ ΤΠ’”κΈΜ÷Ο![]() ÷°ΦδΒΡΙΊœΒΆΦœσΘ§ΆΦ÷–
÷°ΦδΒΡΙΊœΒΆΦœσΘ§ΆΦ÷–![]() ΒψΈΣΆΦœΏΒΡΉνΒΆΒψΘ§
ΒψΈΣΆΦœΏΒΡΉνΒΆΒψΘ§![]() ¥ΠΒΡΉίΉχ±ξ
¥ΠΒΡΉίΉχ±ξ![]() Θ§
Θ§![]() ¥ΠΒΡΉίΉχ±ξΠ’=
¥ΠΒΡΉίΉχ±ξΠ’=![]() Θ§
Θ§![]() ¥ΠΒΡΉίΉχ±ξΠ’=
¥ΠΒΡΉίΉχ±ξΠ’=![]() Θ°»τ‘Ύ
Θ°»τ‘Ύ![]() ΒΡ
ΒΡ![]() Βψ”…Ψ≤÷Ι ΆΖ≈“ΜΗω÷ ΝΩΈΣ
Βψ”…Ψ≤÷Ι ΆΖ≈“ΜΗω÷ ΝΩΈΣ![]() ΓΔΒγΝΩΈΣ
ΓΔΒγΝΩΈΣ![]() ΒΡ¥χΒγΈοΩιΘ®Ω… ”ΈΣ÷ ΒψΘ©Θ§ΈοΩιΥφΦ¥œρ”“‘ΥΕ·Θ°«σΘΚ
ΒΡ¥χΒγΈοΩιΘ®Ω… ”ΈΣ÷ ΒψΘ©Θ§ΈοΩιΥφΦ¥œρ”“‘ΥΕ·Θ°«σΘΚ
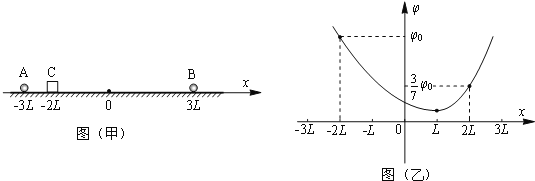
Θ®1Θ©ΙΧΕ®‘Ύ![]() ¥ΠΒΡΒγΚ…ΒΡΒγΝΩ
¥ΠΒΡΒγΚ…ΒΡΒγΝΩ![]() ΘΜ
ΘΜ
Θ®2Θ©ΈΣΝΥ Ι–ΓΈοΩιΡήΙΜΒΫ¥ο![]() ¥ΠΘ§ ‘Χ÷¬έ–ΓΈοΩι”κΥ°ΤΫΟφΦδΒΡΕ·ΡΠ≤Ν“ρ ΐ
¥ΠΘ§ ‘Χ÷¬έ–ΓΈοΩι”κΥ°ΤΫΟφΦδΒΡΕ·ΡΠ≤Ν“ρ ΐ![]() Υυ¬ζΉψΒΡΧθΦΰΘΜ
Υυ¬ζΉψΒΡΧθΦΰΘΜ
Θ®3Θ©»τ–ΓΈοΩι”κΥ°ΤΫΟφΦδΒΡΕ·ΡΠ≤Ν“ρ ΐ![]() Θ§–ΓΈοΩι‘ΥΕ·ΒΫάκAΒψLA¥Π ±Θ§ΥΌΕ»Ήν¥σΘ§–¥≥ωΨύάκLAΒΡΖΫ≥Χ±μ¥ο ΫΘ§≤Δ«σΉν¥σΥΌΕ»
Θ§–ΓΈοΩι‘ΥΕ·ΒΫάκAΒψLA¥Π ±Θ§ΥΌΕ»Ήν¥σΘ§–¥≥ωΨύάκLAΒΡΖΫ≥Χ±μ¥ο ΫΘ§≤Δ«σΉν¥σΥΌΕ»![]() «Εύ…ΌΘΩ(LA=3L)
«Εύ…ΌΘΩ(LA=3L)
ΓΨ¥πΑΗΓΩΘ®1Θ©4QΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©![]()
ΓΨΫβΈωΓΩ
(1)”…ΆΦΘ®““Θ©ΒΟΘ§xΘΫLΒψΈΣΆΦœΏΒΡΉνΒΆΒψΘ§«–œΏ–±¬ ΈΣΝψΘ§Φ¥Κœ≥Γ«ΩEΚœΘΫ0
Υυ“‘ΘΚ![]() Θ§ΒΟ
Θ§ΒΟ![]()
ΫβΒΟΘΚ
QAΘΫ4Q
(2)ΈοΩιœ»ΉωΦ”ΥΌ‘ΥΕ·‘ΌΉωΦθΥΌ‘ΥΕ·Θ§ΒΫ¥οxΘΫ2L¥ΠΥΌΕ»vtΓί0
¥”xΘΫ©¹2LΒΫxΘΫ2LΙΐ≥Χ÷–Θ§”…Ε·ΡήΕ®άμΒΟΘΚ![]()
Φ¥ΘΚ![]()
ΫβΒΟΘΚ
![]()
(3)–ΓΈοΩι‘ΥΕ·ΥΌΕ»Ήν¥σ ±Θ§Βγ≥ΓΝΠ”κΡΠ≤ΝΝΠΒΡΚœΝΠΈΣΝψΘ§…ηΗΟΈΜ÷ΟάκAΒψΒΡΨύάκΈΣlAΘ§‘ρ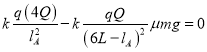
ΫβΒΟΘΚ
lAΘΫ3L
Φ¥–ΓΈοΩι‘ΥΕ·ΒΫxΘΫ0 ±ΥΌΕ»Ήν¥σΓΘ
–ΓΈοΩι¥”xΘΫ©¹2L‘ΥΕ·ΒΫxΘΫ0ΒΡΙΐ≥Χ÷–Θ§”…Ε·ΡήΕ®άμΒΟΘΚ![]()
¥ζ»κ ΐΨίΘΚ
![]()
ΫβΒΟΘΚ
![]()

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ