题目内容
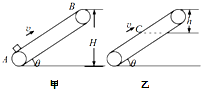 如图所示,甲、乙两种粗糙面不同的传送带,倾斜于水平地面放置,以同样恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传动带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B竖直高度为h的C处时达到传送带的速率v.已知B处离地面的高度皆为H.则在物体从A到B的过程中( )
如图所示,甲、乙两种粗糙面不同的传送带,倾斜于水平地面放置,以同样恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传动带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B竖直高度为h的C处时达到传送带的速率v.已知B处离地面的高度皆为H.则在物体从A到B的过程中( )| A、两种传送带对小物体做功相等 | B、将小物体传送到B处,两种传送带消耗的电能相等 | C、两种传送带与小物体之间的动摩擦因数不同 | D、将小物体传送到B处,两种系统产生的热量不相等 |
分析:小物块从底端上升到顶端过程与上升到速度达到皮带速度过程不同,动能定理表达式不同.本题的关键是比较两种情况下产生的热量关系,难点在于结合v-t图象求出物体位移及相对位移的联系.
解答:解:A、小球在运动过程中受重力和传送带的作用力;对全程由动能定理可得:因高度相等,则重力做功相等;末速度相等,则动能的变化量相等;则由动能定理可得,传送带对物体做功相等;故A正确;
C、甲图中平均速度为
,乙图中位移H-h 的过程中平均速度为
,则可知,乙图中加速时间较短;则由速度公式v=at可知物体加速度关系a甲<a乙,再由牛顿第二定律μmgcosθ-mgsinθ=ma,μ甲<μ乙,故C正确;
D、由摩擦生热Q=fS相对知,
Q甲=f1S1=vt1-
=f1
Q乙=f2S2=f2
根据牛顿第二定律得
f1-mgsinθ=ma1=m
f2-mgsinθ=ma2=m
解得:Q甲=mgH+
mv2,Q乙=mg(H-h)+
mv2,Q甲>Q乙,故D错误;
B、根据能量守恒定律,电动机消耗的电能E电等于摩擦产生的热量Q与物块增加机械能的和,
因物块两次从A到B增加的机械能相同,Q甲>Q乙,所以将小物体传送到B处,两种传送带消耗的电能甲更多,故B错误;
故选:ACD.
C、甲图中平均速度为
| v |
| 2 |
| v |
| 2 |
D、由摩擦生热Q=fS相对知,
Q甲=f1S1=vt1-
| vt1 |
| 2 |
| H |
| sinθ |
Q乙=f2S2=f2
| H-h |
| sinθ |
根据牛顿第二定律得
f1-mgsinθ=ma1=m
| v2 | ||
2
|
f2-mgsinθ=ma2=m
| v2 | ||
2
|
解得:Q甲=mgH+
| 1 |
| 2 |
| 1 |
| 2 |
B、根据能量守恒定律,电动机消耗的电能E电等于摩擦产生的热量Q与物块增加机械能的和,
因物块两次从A到B增加的机械能相同,Q甲>Q乙,所以将小物体传送到B处,两种传送带消耗的电能甲更多,故B错误;
故选:ACD.
点评:解决该题关键要能够对物块进行受力分析,运用运动学公式和牛顿第二定律找出相对位移和摩擦力的关系.并注意传送带消耗电能和摩擦生热的关系及求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 用伏安法测电阻,可采用如图所示的甲、乙两种接法.如所用电压表内阻为5000Ω,电流表内阻为0.5Ω.
用伏安法测电阻,可采用如图所示的甲、乙两种接法.如所用电压表内阻为5000Ω,电流表内阻为0.5Ω. 如图所示,甲、乙两种粗糙面不同的传送带,以相同的倾角放置于水平地面,并以同样恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B竖直高度为h的C处时达到传送带的速率v.已知B处离地面的高度皆为H.则在物体从A到B的过程中( )
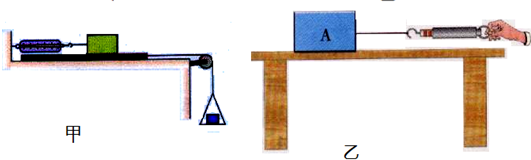
如图所示,甲、乙两种粗糙面不同的传送带,以相同的倾角放置于水平地面,并以同样恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B竖直高度为h的C处时达到传送带的速率v.已知B处离地面的高度皆为H.则在物体从A到B的过程中( ) 如图所示的甲、乙两图表示用同一套器材测量铁块P与长金属板间的滑动摩擦力的两种不同方法.甲图把弹簧秤的一端固定在墙上,用力F水平向右拉金属板,使金属板向右运动;乙图使金属板静止在水平桌面上,用手通过弹簧秤向左用力F拉P,使P向左运动.在如图所示中甲、乙两种方法中,正确的测量方法是
如图所示的甲、乙两图表示用同一套器材测量铁块P与长金属板间的滑动摩擦力的两种不同方法.甲图把弹簧秤的一端固定在墙上,用力F水平向右拉金属板,使金属板向右运动;乙图使金属板静止在水平桌面上,用手通过弹簧秤向左用力F拉P,使P向左运动.在如图所示中甲、乙两种方法中,正确的测量方法是 如图所示,甲、乙两种粗糙面不同的倾斜传送带,以同样恒定的速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B竖直高度为h的C处时达到传送带的速率v.已知B处离地面的高度皆为H,小物体与两种传送带间的动摩擦因数均大于tan θ,则物体在从A运动到B的过程中,下列说法正确的是( )
如图所示,甲、乙两种粗糙面不同的倾斜传送带,以同样恒定的速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B竖直高度为h的C处时达到传送带的速率v.已知B处离地面的高度皆为H,小物体与两种传送带间的动摩擦因数均大于tan θ,则物体在从A运动到B的过程中,下列说法正确的是( )