题目内容
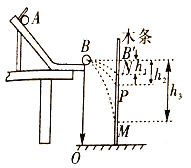
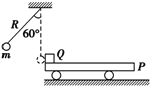
【题目】如图所示,质量为![]() 的平板车P的上表面离地面高
的平板车P的上表面离地面高![]() ,质量为
,质量为![]() 的小物块
的小物块![]() 大小不计,可视为质点
大小不计,可视为质点![]() 位于平板车的左端,系统原来静止在光滑水平地面上,一不可伸长的轻质细绳长为
位于平板车的左端,系统原来静止在光滑水平地面上,一不可伸长的轻质细绳长为![]() ,一端悬于Q正上方高为R处,另一端系一质量也为m的小球
,一端悬于Q正上方高为R处,另一端系一质量也为m的小球![]() 大小不计,可视为质点
大小不计,可视为质点![]() 。今将小球拉至悬线与竖直方向成
。今将小球拉至悬线与竖直方向成![]() 角由静止释放,小球到达最低点时与Q的碰撞时间极短,且无机械能损失。已知Q离开平板车时速度大小
角由静止释放,小球到达最低点时与Q的碰撞时间极短,且无机械能损失。已知Q离开平板车时速度大小![]() ,Q与P之间的动摩擦因数
,Q与P之间的动摩擦因数![]() ,重力加速度
,重力加速度![]() ,计算:
,计算:
![]() 小球与Q碰撞前瞬间,细绳拉力T的大小;
小球与Q碰撞前瞬间,细绳拉力T的大小;
![]() 平板车P的长度L;
平板车P的长度L;
![]() 小物块Q落地时与小车的水平距离s。
小物块Q落地时与小车的水平距离s。
【答案】(1) 20 N (2) 1.75 m (3) 0.1 m
【解析】
(1) 设小球与Q碰前瞬间的速度为v0,小球在下摆过程中,由动能定理有:
![]()
在最低点有![]()
解得v0=![]() =3 m/s,T=20 N
=3 m/s,T=20 N
(2) 小球与Q碰撞后,设小球与Q的速度分别为v0′和vQ.在碰撞过程中
由动量守恒有![]()
由能量守恒有![]()
解得vQ=3 m/s
设Q离开平板车时P的速度为v2,Q与P组成的系统动量守恒
由动量守恒有mvQ=mv1+Mv2
由能量守恒有![]()
解得v2=0.5 m/s,L=1.75 m
(3) Q脱离P后做平抛运动,设做平抛运动的时间为t.
竖直方向有![]()
解得t=0.5 s
Q落地时二者相距s=(v1-v2)t=0.1 m

练习册系列答案
相关题目