题目内容
【题目】如图所示,倾角为37°,的传送带,转动速率恒为v,动摩擦因数μ=0.5,在传送带顶端A处无初速度地释放一个质量为m的物体.已知sin 37°=0.6,cos 37°=0.8,g=10 m/s2.当传送带顺时针转动时,物体从顶端A滑到底端B的时间为t1;当传送带逆时针转动时,物体从顶端A滑到底端B的时间为t2.则

A. t1>t2 B. t1<t2
C. t1 =t2 D. 无法确定,因为v未知
【答案】A
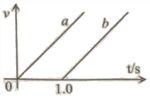
【解析】传送带顺时针转动时,物体相对传送带向下运动,则物体所受滑动摩擦力沿斜面向上,相对传送带向下匀加速运动,由牛顿第二定律得:mg(sin37°-μcos37°)=ma1,解得:a1=2m/s2,传送带逆时针转动,当物体下滑速度小于传送带转动速度时,物体相对传送带向上运动,则物体所受滑动摩擦力沿传送带向下,设物体的加速度大小为a2,由牛顿第二定律得:mgsin37°+μmgcos37°=ma2,代入数据得:a2=10m/s2,由此可知传送带逆时针转动时的加速度大于传送带顺时针转动时的加速度,根据运动学公式![]() ,可知无论物体滑到底端时是否共速都有t1>t2,故A正确,BCD错误。
,可知无论物体滑到底端时是否共速都有t1>t2,故A正确,BCD错误。

练习册系列答案
相关题目