题目内容
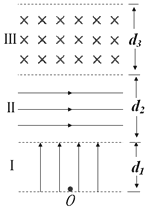
【题目】如图所示空间分为Ⅰ、Ⅱ、Ⅲ 三个足够长的区域,各边界面相互平行。其中Ⅰ、Ⅱ区域存在匀强电场: ![]() V/m,方向垂直边界面竖直向上;EⅡ =
V/m,方向垂直边界面竖直向上;EⅡ = ![]() V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0T,方向垂直纸面向里。三个区域宽度分别为d1=5.0m、d2=4.0m、d3=10m。一质量m=1.0×10-8kg、电荷量q = 1.6×10-6C 的粒子从O点由静止释放,粒子重力忽略不计。求:
V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0T,方向垂直纸面向里。三个区域宽度分别为d1=5.0m、d2=4.0m、d3=10m。一质量m=1.0×10-8kg、电荷量q = 1.6×10-6C 的粒子从O点由静止释放,粒子重力忽略不计。求:
(1)粒子离开区域Ⅰ时的速度
(2)粒子从区域Ⅱ进入区域Ⅲ时的速度方向与边界面的夹角
(3)粒子在Ⅲ区域中作圆周运动的周期和离开Ⅲ区域时的速度方向与边界面的夹角
【答案】(1)4×103 m/s(2)300(3)β=arccos![]()
【解析】
试题分析:(1)由动能定理得:
mv12/2 = qE1 d1 ①
得: v1= 4×103 m/s ②
(2)粒子在区域II做类平抛运动。水平向右为y轴,竖直向上为x轴.设粒子进入区域III时速度与边界的夹角为θ
tanθ = vx/ vy ③
vx = v1 , vy = at ④
a = qE2/m ⑤
t = d2/ v1
把数值代入得:θ = 300 ⑥
(3)粒子在磁场中运动的周期T=![]()
![]() =
=![]()
![]() 10-2 s
10-2 s
粒子进入磁场时的速度v2 = 2 v1 ⑦
粒子在磁场中运动的半径R=m v2 /qB = 10m = d3
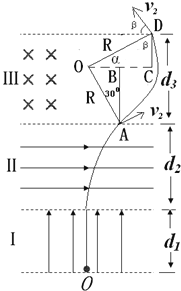
粒子进入磁场区域运动轨迹如图所示,由于
R=![]() = 10 m
= 10 m
AB=5![]() m,CD=(10 — 5
m,CD=(10 — 5![]() )m
)m
cosβ= ![]()
![]() ⑧
⑧
所以粒子离开磁场时速度方向与边界的夹角β=arccos![]() (此关系式不写不扣分)
(此关系式不写不扣分)

练习册系列答案
相关题目