Question

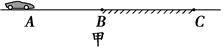
（19分）如图所示，ABCD为固定在竖直平面内的轨道，AB段光滑水平，BC段为光滑圆弧，对应的圆心角θ=37°，半径r=2.5m，CD段平直倾斜且粗糙，各段轨道均平滑连接，倾斜轨道所在区域有场强大小为E=2×10⁵N/C、方向垂直于斜轨向下的匀强电场。质量m=5×10^-2kg、电荷量q=+1×10^-6C的小物体（视为质点）被弹簧枪发射后，沿水平轨道向左滑行，在C点以速度v₀=3m/s冲上斜轨。以小物体通过C点时为计时起点，0.1s以后，场强大小不变，方向反向。已知斜轨与小物体间的动摩擦因数μ=0.25。设小物体的电荷量保持不变，取g=10m/s²，sin37°=0.6，cos37°=0.8。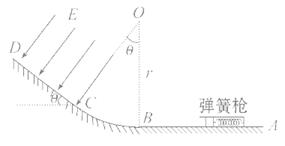

（1）求弹簧枪对小物体所做的功;
（2）在斜轨上小物体能到达的最高点为P，求CP的长度。

Answer 1

（1）0.475J（2）0.57m

解析试题分析：（1）设弹簧枪对小物体做的功为W，由动能定理得
W-mgr（1-cosθ）=mv₀²　  ①
代入数据得W=0.475J     ②
（2）取沿平直斜轨向上为正方向。设小物体通过C点进入电场后的加速度为a₁，由牛顿第二定律得
-mgsinθ-μ（mgcosθ+qE）=ma₁　    ③
小物体向上做匀减速运动，经t₁=0.1s后，速度达到v₁，有
v₁=v₀+a₁t₁　  ④
由③④可知v₁=2.1m/s，设运动的位移为x₁，有
x₁=v₀t₁+a₁t₁²　 ⑤
电场力反向后，设小物体的加速度为a₂，由牛顿第二定律得
-mgsinθ-μ（mgcosθ-qE）=ma₂　  ⑥
设小物体以此加速度运动到速度为0，运动的时间为t₂，位移为x₂，有
0=v₁+a₂t₂　⑦
x₂=v₁t₂+a₂t₂²　⑧
设CP的长度为x，有x=x₁+x₂　 ⑨
联立相关方程，代入数据解得x=0.57m  ⑩
考点：牛顿第二定律及动能定理的应用。