题目内容
19.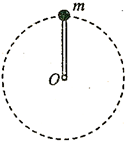 如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,以下说法正确的是(重力加速度为g)( )
如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,以下说法正确的是(重力加速度为g)( )| A. | 小球过最高点时的最小速度为$\sqrt{gR}$ | |
| B. | 小球过最高点时,杆所受的弹力可能等于零 | |
| C. | 小球过最高点时,杆对球的作用力一定小于重力 | |
| D. | 小球过最高点时,杆对球作用力一定与小球所受重力方向相反 |
分析 小球在最高点,杆对球可以表现为支持力,也可以表现为拉力,在最高点的最小速度为零,根据牛顿第二定律分析杆子对小球的作用力与速度的关系.
解答 解:A、由于杆能支撑小球,所以小球过最高点时的最小速度为零,故A错误.
B、小球过最高点时,速度为v=$\sqrt{gR}$时,有mg=m$\frac{{v}^{2}}{R}$,由重力完全提供向心力,杆所受的弹力为零,故B正确.
C、小球过最高点时,当v>$\sqrt{gR}$时,有mg+F=m$\frac{{v}^{2}}{R}$,当v>$\sqrt{2gR}$时,F>mg,故C错误.
D、小球过最高点时,当v>$\sqrt{gR}$时,杆对球作用力与小球所受重力方向相同,故D错误.
故选:B
点评 解决本题的关键知道小球做圆周运动向心力的来源,知道最高点的临界情况,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
14.从静止开始做匀变速直线运动的物体,在第2s内通过的位移是6m,则前3s内所通过的位移是( )
| A. | 10m | B. | 12m | C. | 18m | D. | 25m |
4.一电荷只在电场力的作用下从A点运动的B点,下列说法正确的是( )


| A. | 电场力一定做正功 | B. | 电场力一定做负功 | ||
| C. | A点的电势比B点高 | D. | 电荷一定做加速运动 |