题目内容
1.通信卫星(同步卫星)总是“停留”在赤道上空的某处.已知地球质量为M,半径为R,自转周期为T,万有引力恒量为G,则同步卫星周期是T,离地面的高度h=\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}-R.分析 根据地球的同步卫星的万有引力提供向心力,可以求出地球同步卫星的高度,从而即可求解.
解答 解:地球同步卫星的周期等于地球的自转周期T,根据引力提供向心力,则对地球同步卫星有:
GMm(R+h)2=m4π2T2(R+h)
解得:h=\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}-R
故答案为:T,\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}-R.
点评 解答此题要清楚地球的同步卫星的万有引力提供向心力,由万有引力定律和向心力公式结合研究.

练习册系列答案
相关题目
19.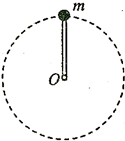 如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,以下说法正确的是(重力加速度为g)( )
如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,以下说法正确的是(重力加速度为g)( )
 如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,以下说法正确的是(重力加速度为g)( )
如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,以下说法正确的是(重力加速度为g)( )| A. | 小球过最高点时的最小速度为√gR | |
| B. | 小球过最高点时,杆所受的弹力可能等于零 | |
| C. | 小球过最高点时,杆对球的作用力一定小于重力 | |
| D. | 小球过最高点时,杆对球作用力一定与小球所受重力方向相反 |
12.关于电磁场理论和电磁波,下列说法正确的是( )
| A. | 在电场周围一定产生磁场,磁场周围一定产生电场 | |
| B. | 在变化的电场周围一定产生磁场,变化的磁场周围一定产生电场 | |
| C. | 电磁场是一种物质,其传播的速度总是3×108m/s | |
| D. | 电磁波由真空传入介质,速度变小,频率变小 |
6.用红光进行双缝干涉实验时(缝极窄),如果用不透光的纸遮住一个缝,则屏上出现( )
| A. | 一片黑暗 | B. | 一片红光 | ||
| C. | 原干涉条纹形状不变,但亮度减弱 | D. | 红、黑相间的条纹 |
13.下列说法正确的是( )
| A. | 信阳市城区出租车收费标准为1.4元/公里,这里的“公里”指的是位移 | |
| B. | 在国际单位制中质量的单位是克 | |
| C. | 速度变化量大,加速度不一定大 | |
| D. | 匀速圆周运动是匀变速曲线运动 |
11. 半径为R的均匀带电球体,在通过球心O的直线上,各点的电场分布如图所示.当x≥R时.电场分布与电荷量全部集中在球心时相同.已知静电力常量为k.则( )
半径为R的均匀带电球体,在通过球心O的直线上,各点的电场分布如图所示.当x≥R时.电场分布与电荷量全部集中在球心时相同.已知静电力常量为k.则( )
 半径为R的均匀带电球体,在通过球心O的直线上,各点的电场分布如图所示.当x≥R时.电场分布与电荷量全部集中在球心时相同.已知静电力常量为k.则( )
半径为R的均匀带电球体,在通过球心O的直线上,各点的电场分布如图所示.当x≥R时.电场分布与电荷量全部集中在球心时相同.已知静电力常量为k.则( )| A. | 球面是个等势面,球体是个等势体 | B. | 在x轴上x=R处电势最高 | ||
| C. | xP=√2R | D. | 球心O与球面间的电势差为E0R |