Question

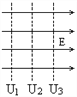
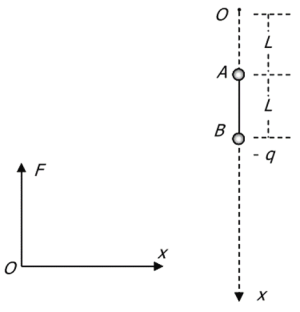
【题目】空间有一静电场，在x轴上的电场方向竖直向下，轴上的电场强度大小按 E＝kx分布（x是轴上某点到 O点的距离），如图所示。在O点正下方有一长为L的绝缘细线连接 A、B两个均带负电的小球（可视为质点），A 球距O点的距离为L，两球恰好静止，细绳处于张紧状态。已知 A、B 两球质量均为m,B所带电量为-q，k ，不计两小球之间的静电力作用。

（1）求A球的带电量；

（2）画出 A 球所受电场力F 与x的图像；剪断细线后，A球向上运动，求A球运动的最大速度vm；（提示：借助 F-x图像可以确定电场力做功的规律）

（3）剪断细线后，求B球的运动范围。

Answer 1

【答案】(1)(2)，(3)

【解析】

(1)A、B两球静止时，A球所处位置场强为

B球所处位置场强为

对A、B由整体法得

解得

(2)A球所受电场力F与x的图像如图所示

剪断细线后，A球向上运动，当A球的加速度为零时，速度达到最大，此时A球距O点距离为：

解得

剪断细线后，A球从运动到获得最大速度，A球上升的高度为

由动能定理得

由图像可知，可得

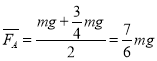
解得

(3)剪断细线后，设B球向下运动的最大位移为△x时，速度变为零，此时B球所受电场力为

由动能定理得

则有

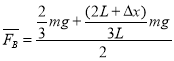
解得

则B球的运动范围是