��Ŀ����
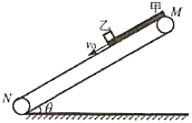
����Ŀ����ͼ1��ʾ���⻬��ƽ����ֱ��������AB��CD���L����A��C֮���һ����ֵΪR�ĵ��裬���������abcd�����������д�ֱ����ƽ����ֱ���ϡ���Ϊ5d����ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊm������Ϊr������Ҳ�պ�ΪL�ĵ�������ڴų��±߽�ab�ϣ���ab���غϣ�������һ����ֱ���ϵ���F���������ʹ���ɾ�ֹ��ʼ�˶�����֪������뿪�ų�ǰ�ѿ�ʼ������ֱ���˶���������뵼��ʼ�մ�ֱ�ұ������ýӴ���������費�ƣ�F�浼������ʼλ�õľ���x�仯�������ͼ2��ʾ�������ж���ȷ���ǣ� ��
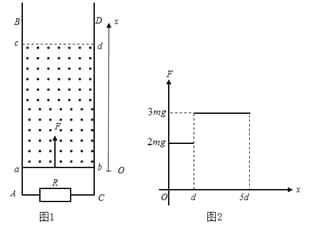
A. ������뿪�ų�ʱ�ٶȴ�СΪ![]()
B. ����������ų��Ĺ����У�ͨ������R�ĵ����Ϊ![]()
C. �뿪�ų�ʱ��������˵�ѹΪ![]()
D. ����������ų��Ĺ����У�����R����������Ϊ![]()
���𰸡�ACD
��������
�����赼����뿪�ų�ʱ�ٶȴ�СΪv����ʱ������ܵ��İ�������СΪ��![]() ����ƽ�������ã�F=F��+mg����ͼ2֪��F=3mg��������ã�
����ƽ�������ã�F=F��+mg����ͼ2֪��F=3mg��������ã�![]() ����A��ȷ������������ų��Ĺ����У�ͨ������R�ĵ����Ϊ��
����A��ȷ������������ų��Ĺ����У�ͨ������R�ĵ����Ϊ��![]() ����B�����뿪�ų�ʱ����F=BIL+mg�ã�
����B�����뿪�ų�ʱ����F=BIL+mg�ã�![]() ����������˵�ѹΪ��
����������˵�ѹΪ��![]() ����C��ȷ������������ų��Ĺ����У����·�������ܽ�����ΪQ�����ݹ��ܹ�ϵ�ɵã�Q=WF-mg5d-
����C��ȷ������������ų��Ĺ����У����·�������ܽ�����ΪQ�����ݹ��ܹ�ϵ�ɵã�Q=WF-mg5d-![]() mv2
mv2
������������WF=2mgd+3mg4d=14mgd
����R����������Ϊ��![]() ������ã�
������ã�![]() ����D��ȷ��
����D��ȷ��
��ѡACD��

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�