题目内容
9.如图甲所示,在气垫导轨的左端固定一轻质弹簧,轨道上有一滑块A紧靠弹簧但不连接,已知滑块的质量为m.
(1)用游标卡尺测出滑块A上的挡光片的宽度,度数如图乙所示,则宽度d=5.10;
(2)为探究弹簧的弹性势能,某同学打开气源,用力将滑块A压到P点,然后释放,滑块A上的挡光片通过光电门的时间为t,则弹簧的弹性势能的表达式为${E}_{P}=\frac{1}{2}m{v}^{2}=\frac{1}{2}m{(\frac{d}{△t})}^{2}$(用题中所给字母表示);
(3)若弹簧的弹性势能与劲度系数k以及弹簧的形变量x的关系为:Ep=$\frac{1}{2}$kx2,打开气源,将滑块从A由静止释放,光电门到P点的距离为x时,测出滑块上的挡光片通过光电门的时间为t,移动光电门,测出多组数据(滑块都能通过光电门),并绘出x-$\frac{1}{t}$图象,如图丙所示,已知该图线的斜率绝对值为k′,则可算出弹簧的劲度系数为k=$\frac{{d}^{2}}{2gk}$.
分析 (1)先读主尺,在读游标尺,游标尺不能估读,那个对齐就读那个.
(2)由滑块A上的挡光片通过光电门的时间可得此时滑块的平均速度,由于滑块此阶段做匀速运动,故瞬时速度等于平均速度,由能量转化和守恒可得弹簧弹性势能.
(3)每次都有P释放,则每次弹簧弹性势能都相同,由能量转化和守恒可得结果.
解答 解:(1)主尺读数为:5mm;游标尺分度为0.05mm,第2个刻度对齐,故游标尺读数为:0.05×2mm=0.10mm,故宽度为:d=5+0.10=5.10mm.
(2)滑块通过光电门已经是匀速运动了,其平均速度为:$\overline{v}=\frac{d}{△t}$,瞬时速度等于平均速度,故瞬时速度为:$v=\frac{d}{△t}$,此时滑块动能全部由弹簧弹性势能转化而来,故弹簧弹性势能为:${E}_{P}=\frac{1}{2}m{v}^{2}=\frac{1}{2}m{(\frac{d}{△t})}^{2}$.
(3)每次都有P释放,则每次弹簧弹性势能都相同,由能量转化和守恒可得:
$\frac{1}{2}m{(\frac{d}{{t}_{1}})}^{2}+μmg{x}_{1}=\frac{1}{2}m{(\frac{d}{{t}_{2}})}^{2}+μmg{x}_{2}$ ①
解得:
$μ=-\frac{{d}^{2}}{2g}(\frac{\frac{1}{{{t}_{2}}^{2}}-\frac{1}{{{t}_{1}}^{2}}}{{x}_{2}-{x}_{1}})$ ②
由于$k=\frac{x}{\frac{1}{{t}^{2}}}$,故$\frac{\frac{1}{{{t}_{2}}^{2}}-\frac{1}{{{t}_{1}}^{2}}}{{x}_{2}-{x}_{1}}=-\frac{1}{k}$,带入可得:
$μ=\frac{{d}^{2}}{2gk}$
故答案为:(1)5.10;(2)$\frac{1}{2}m(\frac{d}{△t})^{2}$;(3)$\frac{d^2}{2gk}$
点评 本题考查弹簧的弹性势能决定因素的验证;主要难点在第3问,这里用到的方法比较不容易想到,整体难度较大,且易错.

 习题精选系列答案
习题精选系列答案| A. | 速度变化的大小可能小于2m/s | B. | 加速度的大小可能小于1m/s2 | ||
| C. | 平均速度的大小可能小于3m/s | D. | 位移的大小可能大于6m |
 如图所示为电磁轨道炮的工作原理图.待发射弹体与轨道保持良好接触,并可在两平行轨道之间无摩擦滑动.电流从一条轨道流入,通过弹体流回另一条轨道.轨道电流在弹体处形成垂直于轨道平面的磁场(可视为匀强磁场),磁感应强度的大小与电流强度I成正比.弹体在安培力的作用下滑行L后离开轨道.离开轨道时的速度大小为v0.为使弹体射出时的速度变为2v0,理论上可采用的方法有( )
如图所示为电磁轨道炮的工作原理图.待发射弹体与轨道保持良好接触,并可在两平行轨道之间无摩擦滑动.电流从一条轨道流入,通过弹体流回另一条轨道.轨道电流在弹体处形成垂直于轨道平面的磁场(可视为匀强磁场),磁感应强度的大小与电流强度I成正比.弹体在安培力的作用下滑行L后离开轨道.离开轨道时的速度大小为v0.为使弹体射出时的速度变为2v0,理论上可采用的方法有( )| A. | 只将轨道长度L变为原来的2倍 | B. | 只将电流I变为原来的2倍 | ||
| C. | 只将电流I变为原来的4倍 | D. | 只将弹体质量变为原来的2倍 |
 如图,P和Q为带电量分别为+q和-q的两个等量异种电荷,两者相距L,O为PQ连线的中点,M、N为中垂线上关于O点对称的两个点,则( )
如图,P和Q为带电量分别为+q和-q的两个等量异种电荷,两者相距L,O为PQ连线的中点,M、N为中垂线上关于O点对称的两个点,则( )| A. | M,O,N三点的场强都相等 | |
| B. | M、N 两点的场强大小相等,方向相同 | |
| C. | O点的场强为零 | |
| D. | 带电粒子仅受电场力作用由N运动到M动能保持不变 |
| A. | 它们受到的空气阻力对运动的影响相同 | |
| B. | 忽略空气阻力,它们的加速度相等 | |
| C. | 忽略空气阻力,它们落地的速度不等 | |
| D. | 忽略空气阻力,它们下落的时间相等 |
| A. | 出租车出发后最快经72.5s追上班车 | |
| B. | 出租车出发后最快经132.5s追上班车 | |
| C. | 出租车追上班车时距离车站2500m | |
| D. | 出租车追上班车时距离车站2400m |
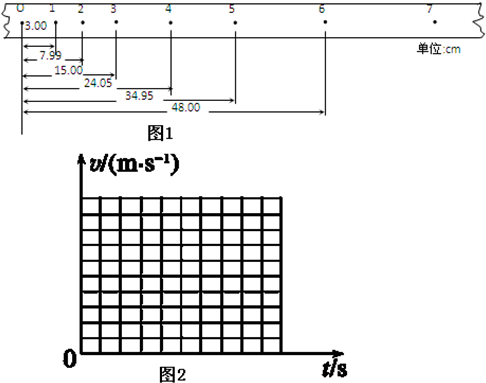
(1)根据上面记录,计算打点计时器在各点的速度并把下表填充完整.
| 位置 | 1 | 2 | 3 | 4 | 5 |
| V/(m•s-1) | 0.40 |
 一位链球运动员在水平面内旋转质量为m=4kg的链球,链球做匀速圆周运动且周期T=1s,转动半径为r=2.0m.求:
一位链球运动员在水平面内旋转质量为m=4kg的链球,链球做匀速圆周运动且周期T=1s,转动半径为r=2.0m.求: 如图所示,质量为m=0.3kg的小球,带电量为q=-$\sqrt{3}$×10-3C,用绝缘细线悬挂于水平方向匀强电场中.小球静止时,细线与竖直方向成θ=30°角,求小球所处匀强电场的场强大小及方向.(g=10m/s2)
如图所示,质量为m=0.3kg的小球,带电量为q=-$\sqrt{3}$×10-3C,用绝缘细线悬挂于水平方向匀强电场中.小球静止时,细线与竖直方向成θ=30°角,求小球所处匀强电场的场强大小及方向.(g=10m/s2)