题目内容
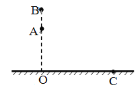
【题目】如图所示,长度为L的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略).已知重力加速度为g.
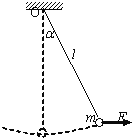
(1)在水平拉力F的作用下,轻绳与竖直方向的夹角为α,小球处于平衡状态.求力F的大小;
(2)由图示位置无初速释放小球,求当小球第一次通过最低点时的速度及轻绳对小球的拉力(不计空气阻力).
【答案】(1)力F的大小为mgtanα.
(2)小球第一次通过最低点时的速度v=![]() ,轻绳对小球的拉力mg(3﹣2cosα).
,轻绳对小球的拉力mg(3﹣2cosα).
【解析】
试题分析:(1)小球受重力、绳子的拉力和水平拉力平衡,根据共点力平衡求出力F的大小.
(2)根据机械能守恒定律求出小球第一次到达最低点的速度,再根据牛顿第二定律,小球重力和拉力的合力提供向心力,求出绳子拉力的大小.
解:(1)根据平衡条件,应满足Tcosα=mg,Tsinα=F,
拉力大小F=mgtanα;
(2)运动中只有重力做功,根据机械能守恒:mgL(1﹣cosα)=![]() mv2,
mv2,
则通过最低点时:小球的速度大小v=![]() ,
,
方向水平向左;
根据牛顿第二定律:T﹣mg=![]() ,
,
绳子对小球的拉力:T=mg+![]() =mg(3﹣2cosα),
=mg(3﹣2cosα),
方向竖直向上.
答:(1)力F的大小为mgtanα.
(2)小球第一次通过最低点时的速度v=![]() ,轻绳对小球的拉力mg(3﹣2cosα).
,轻绳对小球的拉力mg(3﹣2cosα).

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目