题目内容
8. 如图所示,绷紧的传送带,在电动机的带动下,始终保持v0=2m/s的速度匀速运行,传送带与水平面成30°角,现把质量为m=10kg的工件轻轻放在传送带底端,经过一段时间后,工件被送到高h=2m的平台上,已知工件与传送带的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,若不计其他损耗,g取10m/s2,在传送工件的过程中,电动机消耗的电能是多少?
如图所示,绷紧的传送带,在电动机的带动下,始终保持v0=2m/s的速度匀速运行,传送带与水平面成30°角,现把质量为m=10kg的工件轻轻放在传送带底端,经过一段时间后,工件被送到高h=2m的平台上,已知工件与传送带的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,若不计其他损耗,g取10m/s2,在传送工件的过程中,电动机消耗的电能是多少?
分析 要分析工件的运动情况,首先分析工件的受力情况,工件受到重力、支持力和沿斜面向上的摩擦力作用,合力沿斜面向上,物体加速运动,由牛顿第二定律求出加速度.由运动学公式求出物体速度达到与传送带相同时通过的位移,再根据此位移与传送带长度的关系,分析接下来工件的运动情况;电动机消耗的能量转化为工件的动能和重力势能以及摩擦产生的内能,然后求和即可.
解答 解:工件在传送带上受滑动摩擦为 Ff=μmgcos30°,方向沿斜面向上
工件运动的加速度:a=$\frac{{F}_{f}-mgsin30°}{m}$=g(μcos30°-sin30°)=2.5 m/s2;
其速度达到2 m/s时的位移为:L1=$\frac{{v}_{0}^{2}}{2a}$=$\frac{{2}^{2}}{2×2.5}$m=0.8 m,用时:t=$\frac{{v}_{0}}{a}$=$\frac{2}{2.5}$s=0.8s
此时传送带位移为:L2=v0t=1.6 m
此后工件随传送带一起匀速运动.整个过程中,系统内能的增加量为:
Q=Ff(L2-L1)=μmgcos30°(L2-L1)=60J
物体获得的机械能为:△E=$\frac{1}{2}m{v}_{0}^{2}$+mgh=220J,
所以电动机消耗的电能为:E=Q+△E=280J.
答:在传送工件的过程中,电动机消耗的电能是280J.
点评 本题的解题关键是根据受力情况分析工件的运动情况,再由牛顿第二定律和运动学公式结合求解位移,即可轻松求出功.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 如图所示是一火警器的一部分电路示意图,其中R2为半导体热敏材料(随温度上升时电阻减小)制成的传感器,电流表为值班室的显示器,a、b之间接报警器,当传感器R2所在处出现火情时,显示器的电流I、报警器两端的电压U的变化情况是( )
如图所示是一火警器的一部分电路示意图,其中R2为半导体热敏材料(随温度上升时电阻减小)制成的传感器,电流表为值班室的显示器,a、b之间接报警器,当传感器R2所在处出现火情时,显示器的电流I、报警器两端的电压U的变化情况是( )
 如图所示是一火警器的一部分电路示意图,其中R2为半导体热敏材料(随温度上升时电阻减小)制成的传感器,电流表为值班室的显示器,a、b之间接报警器,当传感器R2所在处出现火情时,显示器的电流I、报警器两端的电压U的变化情况是( )
如图所示是一火警器的一部分电路示意图,其中R2为半导体热敏材料(随温度上升时电阻减小)制成的传感器,电流表为值班室的显示器,a、b之间接报警器,当传感器R2所在处出现火情时,显示器的电流I、报警器两端的电压U的变化情况是( )| A. | I变大 | B. | I变小 | C. | U变大 | D. | U变小 |
19. 如图装置A、B轮通过皮带传动,A、C轮通过摩擦传动,半径RA=2RB=3RC,各接触面均不打滑,则A,B,C三点的线速度和角速度之比分别为( )
如图装置A、B轮通过皮带传动,A、C轮通过摩擦传动,半径RA=2RB=3RC,各接触面均不打滑,则A,B,C三点的线速度和角速度之比分别为( )
 如图装置A、B轮通过皮带传动,A、C轮通过摩擦传动,半径RA=2RB=3RC,各接触面均不打滑,则A,B,C三点的线速度和角速度之比分别为( )
如图装置A、B轮通过皮带传动,A、C轮通过摩擦传动,半径RA=2RB=3RC,各接触面均不打滑,则A,B,C三点的线速度和角速度之比分别为( )| A. | vA:vB:vC=1:2:3,ωA:ωB:ωC=3:2:1 | B. | vA:vB:vC=1:1:1,ωA:ωB:ωC=2:3:6 | ||
| C. | vA:vB:vC=1:1:1,ωA:ωB:ωC=3:2:1 | D. | vA:vB:vC=3:2:1,ωA:ωB:ωC=1:1:1 |
16.关于功率,下列说法中正确的是( )
| A. | 功率是说明力做功多少的物理量 | B. | 力做功越多,功率一定大 | ||
| C. | 功率是说明力做功快慢的物理量 | D. | 做功时间越长,功率一定小 |
3.牛顿发现了万有引力定律后,在一段较长的时间内还不能真正得到应用,主要是万有引力常量G的测量遇到了困难,下列说法正确的是( )
| A. | G的量值与天体的质量有关 | |
| B. | G的量值是牛顿发现万有引力定律后,他经过几年的努力才测出的 | |
| C. | G的量值是由卡文迪许测出的 | |
| D. | G的量值6.67×10-11N•m2/kg2,只适用于计算天体间的万有引力 |
13. 如图为卢瑟福和他的同事们做α 粒子散射实验装置的示意图,荧光屏和显微镜一起分别放在图中的A、B、C、D四个位置时,关于观察到的现象,下述说法中正确的是( )
如图为卢瑟福和他的同事们做α 粒子散射实验装置的示意图,荧光屏和显微镜一起分别放在图中的A、B、C、D四个位置时,关于观察到的现象,下述说法中正确的是( )
 如图为卢瑟福和他的同事们做α 粒子散射实验装置的示意图,荧光屏和显微镜一起分别放在图中的A、B、C、D四个位置时,关于观察到的现象,下述说法中正确的是( )
如图为卢瑟福和他的同事们做α 粒子散射实验装置的示意图,荧光屏和显微镜一起分别放在图中的A、B、C、D四个位置时,关于观察到的现象,下述说法中正确的是( )| A. | 相同时间内放在A位置时观察到屏上的闪光次数最少 | |
| B. | 放在D位置时屏上仍能观察到一些闪光,但次数极少 | |
| C. | 相同时间内放在B位置时观察到屏上的闪光次数比放在A位置时稍少些 | |
| D. | 放在C、D位置时屏上观察不到闪光 |
20.关于竖直上抛运动,下列说法正确的是( )
| A. | 竖直上抛运动先后两次经过同一点时速度相同 | |
| B. | 竖直上抛运动的物体从某点到最高点和从最高点回到该点的时间不相等 | |
| C. | 在最高点速度为零,物体处于平衡状态 | |
| D. | 上升和下降过程的加速度相同 |
17.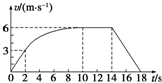 某兴趣小组对一辆自制遥控小车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行,小车的质量为1.0kg,可认为在整个运动过程中小车所受的阻力大小不变.则下列说法不正确的是( )
某兴趣小组对一辆自制遥控小车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行,小车的质量为1.0kg,可认为在整个运动过程中小车所受的阻力大小不变.则下列说法不正确的是( )
 某兴趣小组对一辆自制遥控小车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行,小车的质量为1.0kg,可认为在整个运动过程中小车所受的阻力大小不变.则下列说法不正确的是( )
某兴趣小组对一辆自制遥控小车的性能进行研究.他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段图象为曲线外,其余时间段图象均为直线).已知在小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行,小车的质量为1.0kg,可认为在整个运动过程中小车所受的阻力大小不变.则下列说法不正确的是( )| A. | 小车受到的阻力大小为1.5 N | B. | 小车加速阶段的功率为9 W | ||
| C. | 小车匀速行驶阶段的功率为9 W | D. | 小车加速过程中位移大小为42 m |
18. 小时候,大人们经常给我们讲“龟兔赛跑”的故事. 如图所示是兔子和乌龟在比赛过程中的位移-时间(即x-t)图象,它们的起点和终点相同,由图可知( )
小时候,大人们经常给我们讲“龟兔赛跑”的故事. 如图所示是兔子和乌龟在比赛过程中的位移-时间(即x-t)图象,它们的起点和终点相同,由图可知( )
 小时候,大人们经常给我们讲“龟兔赛跑”的故事. 如图所示是兔子和乌龟在比赛过程中的位移-时间(即x-t)图象,它们的起点和终点相同,由图可知( )
小时候,大人们经常给我们讲“龟兔赛跑”的故事. 如图所示是兔子和乌龟在比赛过程中的位移-时间(即x-t)图象,它们的起点和终点相同,由图可知( )| A. | 兔子和乌龟是从同一时刻出发的 | |
| B. | 兔子和乌龟在比赛途中t2、t4时刻的速度相等 | |
| C. | 乌龟做的是直线运动,兔子是沿折线运动的 | |
| D. | 乌龟先通过预定位移x3到达终点 |